Question

5．在Rt△ABC中，∠C=90°，AB=4，∠ABC=30°，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOB=∠COB=120°，按下列要求画图：以点B为旋转中心，将△AOB绕点B逆时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），回答下列问题：
（1）求∠A′BC的度数；
（2）求OA+OB+OC的值．

Answer 1

分析 （1）首先作出图形，然后求出∠ABA′=60°，即可求出∠A′BC的度数；
（2）首先求出BC的长，然后证明C、O、A′、O′四点共线，即可得到△A′BC是直角三角形，利用勾股定理求出A′C的长，进而求出OA+OB+OC的值．

解答 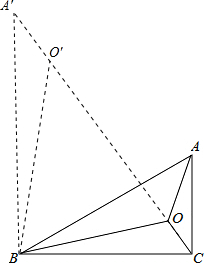解：（1）△A′O′B如图所示；
∵△AOB绕点B逆时针方向旋转60°，∠ABC=30°，
∴∠A′BC=∠ABC+60°=30°+60°=90°，
（2）∵∠C=90°，AB=4，∠ABC=30°，
∴BC=2$\sqrt{3}$，
∵△AOB绕点B逆时针方向旋转60°，得到△A′O′B，
∴A′B=AB=4，BO=BO′，A′O′=AO，
∴△BOO′是等边三角形，
∴BO=OO′，∠BOO′=∠BO′O=60°，
∵∠AOC=∠COB=∠BOA=120°，
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°，
∴C、O、A′、O′四点共线，
∴△A′BC是直角三角形，
∴BC²+A′B²=A′C²，
∴A′C=$\sqrt{（2\sqrt{3}）^{2}+{4}^{2}}$=2$\sqrt{7}$，
∴OA+OB+OC=A′C′+O′O+OC=A′C=2$\sqrt{7}$．

点评 本题考查了利用旋转变换作图，旋转变换的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，勾股定理，等边三角形的判定与性质，综合性较强，最后一问求出C、O、A′、O′四点共线是解题的关键．