题目内容
19. 已知,如图,在直角坐标系中,点M(2,2),一直角三角板直角顶点与点M重合,两直角边分别与x轴正半轴、y轴正半轴交于点A、B,则OA+OB的值是否会发生变化?若不变,求出其值;若变化,求其变化的范围.
已知,如图,在直角坐标系中,点M(2,2),一直角三角板直角顶点与点M重合,两直角边分别与x轴正半轴、y轴正半轴交于点A、B,则OA+OB的值是否会发生变化?若不变,求出其值;若变化,求其变化的范围.
分析 作MC⊥y轴于C,作MD⊥x轴于D,则四边形OCMD是正方形,得出OD=OC=MC=MD=2,∠CMD=90°,证出∠AMD=∠BMC,由ASA证明△AMD≌△BMC,得出AD=BC,即可得出结果.
解答 解:OA+OB的值不发生变化;理由如下:
作MC⊥y轴于C,作MD⊥x轴于D,如图所示: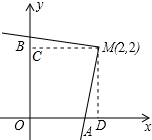 则MC=MD=2,四边形OCMD是正方形,∠BCM=∠ADM=90°,
则MC=MD=2,四边形OCMD是正方形,∠BCM=∠ADM=90°,
∴OD=OC=MC=MD=2,∠CMD=90°,
∵∠AMB=90°,
∴∠AMD=∠BMC,
在△AMD和△BMC中,
$\left\{\begin{array}{l}{∠ADM=∠BCM}&{\;}\\{MD=MC}&{\;}\\{∠AMD=∠BMC}&{\;}\end{array}\right.$,
∴△AMD≌△BMC(ASA),
∴AD=BC,
∴OA+OB=OA+BC+OC=OA+AD+OC=OD+OC=4.
点评 本题考查了坐标与图形性质、全等三角形的判定与性质、正方形的判定与性质;通过作辅助线得出正方形和三角形全等是解决问题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
7.二次函数y=(x-1)(x-2)-1与x轴的交点x1,x2,x1<x2,则下列结论正确的是( )
| A. | x1<1<x2<2 | B. | x1<1<2<x2 | C. | x2<x1<1 | D. | 2<x1<x2 |
9. 如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( )
如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( )
 如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( )
如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( )| A. | $\sqrt{7}$ | B. | 3 | C. | 4 | D. | 5 |
 如图,C为线段AB上一动点,分别过点A、B作DA⊥AB,EB⊥AB.已知AD=3,BE=2,AB=12,设AC=x
如图,C为线段AB上一动点,分别过点A、B作DA⊥AB,EB⊥AB.已知AD=3,BE=2,AB=12,设AC=x 如图,△ABC和△AMN均为等边三角形,边长分别为$\sqrt{3}$,1.连接BM,CM,若BM⊥AC.
如图,△ABC和△AMN均为等边三角形,边长分别为$\sqrt{3}$,1.连接BM,CM,若BM⊥AC.