题目内容
对于二次函数y=x2-2ax+2a+3,分别满足下列条件,求系数a的值.
(1)函数的最小值为零;
(2)当x>5时,y随x增大而增大,且x<5时,y随x增大而减小;
(3)图象在x轴上截得的线段长是3.
(1)函数的最小值为零;
(2)当x>5时,y随x增大而增大,且x<5时,y随x增大而减小;
(3)图象在x轴上截得的线段长是3.
考点:抛物线与x轴的交点,二次函数的性质,二次函数的最值
专题:
分析:(1)可化为顶点为式求得顶点坐标,可求得最小值,令最小值为0,可求得a的值;
(2)由条件可知其对称轴为x=5,代入可求得a的值;
(3)令y=0,所得一元二次方程的两根为二次函数与x轴交点的横坐标,根据根与系数的关系可表示出两点间的线段长度,可求得a.
(2)由条件可知其对称轴为x=5,代入可求得a的值;
(3)令y=0,所得一元二次方程的两根为二次函数与x轴交点的横坐标,根据根与系数的关系可表示出两点间的线段长度,可求得a.
解答:解:(1)∵y=x2-2ax+2a+3=(x-a)2-a2+2a+3,
∴其最小值为-a2+2a+3,
令其为0,可得-a2+2a+3=0,
解得a=3或-1;
(2)由(1)可知二次函数对称轴为x=a,
∵当x>5时,y随x增大而增大,且x<5时,y随x增大而减小,
∴其对称轴为x=5,
∴a=5;
(3)令y=0可得x2-2ax+2a+3=0,
设该方程的两根分别为m,n,
则m+n=2a,mn=2a+3,
∴(m-n)2=(m+n)2-4mn=4a2-8a-12,
根据题意可知(m-n)2=32=9,
即4a2-8a-12=9,解得a=
或-
.
∴其最小值为-a2+2a+3,
令其为0,可得-a2+2a+3=0,
解得a=3或-1;
(2)由(1)可知二次函数对称轴为x=a,
∵当x>5时,y随x增大而增大,且x<5时,y随x增大而减小,
∴其对称轴为x=5,
∴a=5;
(3)令y=0可得x2-2ax+2a+3=0,
设该方程的两根分别为m,n,
则m+n=2a,mn=2a+3,
∴(m-n)2=(m+n)2-4mn=4a2-8a-12,
根据题意可知(m-n)2=32=9,
即4a2-8a-12=9,解得a=
| 7 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查二次函数的最值、增减性及与一元二次方程的关系,掌握二次函数的顶点式y=a(x-h)2+k的顶点坐标为(h,k)、对称轴为x=h是解题的关键.

练习册系列答案
相关题目
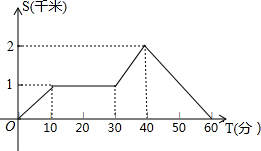 星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )
星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )| A、从家出发,休息一会,就回家 |
| B、从家出发,一直散步(没有停留),然后回家 |
| C、从家出发,休息一会,返回用时20分钟 |
| D、从家出发,休息一会,继续行走一段,然后回家 |
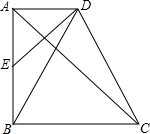 如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线
如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线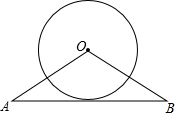 已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切.
已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切. 如图,东西方向的海岸线上有A、B两码头,相距100(
如图,东西方向的海岸线上有A、B两码头,相距100( 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论. 如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2
如图,已知⊙O的半径为6cm,射线PM经过点O,∠MPN=30°,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以2