题目内容
12. 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,EF=4,则CD=4.
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,EF=4,则CD=4.
分析 根据三角形中位线定理证明EF=$\frac{1}{2}$AB,根据直角三角形斜边上的中线等于斜边的一半证明CD=$\frac{1}{2}$AB,进而可求出CD的长.
解答 解:
∵E、F分别为AC、BC的中点,
∴EF=$\frac{1}{2}$AB,
∴AB=8,
在Rt△ABC中,D是AB的中点,
∴CD=$\frac{1}{2}$AB=4,
故答案为:4.
点评 本题考查的是三角形中位线定理和直角三角形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半和直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
2. 如图,直线AB、CD相交于O,EO⊥AB,则∠1与∠2的关系是( )
如图,直线AB、CD相交于O,EO⊥AB,则∠1与∠2的关系是( )
 如图,直线AB、CD相交于O,EO⊥AB,则∠1与∠2的关系是( )
如图,直线AB、CD相交于O,EO⊥AB,则∠1与∠2的关系是( )| A. | 相等 | B. | 对顶角 | C. | 互余 | D. | 互补 |
4.在3,2,-1,-4这四个数中,比-2小的数是( )
| A. | -4 | B. | -1 | C. | 2 | D. | 3 |
 如图,⊙O1与⊙O2相交于A、B两点,过A任作一直线与⊙O1交于M,与⊙O2交于N,问什么时候MN最长?为什么?
如图,⊙O1与⊙O2相交于A、B两点,过A任作一直线与⊙O1交于M,与⊙O2交于N,问什么时候MN最长?为什么?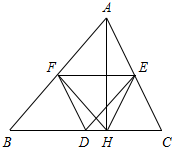 已知:如图,在△ABC中,AH⊥BC于点H,点D,E,F分别是BC,AC,AB的中点.若∠A的度数是α,则图中度数等于α的角还有4个.
已知:如图,在△ABC中,AH⊥BC于点H,点D,E,F分别是BC,AC,AB的中点.若∠A的度数是α,则图中度数等于α的角还有4个.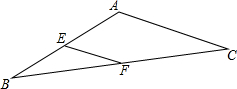 如图在△ABC中,AB=5,BC=7,EF是的中位线,则EF的长度范围是1<EF<6.
如图在△ABC中,AB=5,BC=7,EF是的中位线,则EF的长度范围是1<EF<6.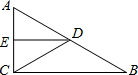 如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.
如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12. 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.