Question

20．如图，⊙O₁与⊙O₂相交于A、B两点，过A任作一直线与⊙O₁交于M，与⊙O₂交于N，问什么时候MN最长？为什么？

Answer 1

分析 结论：设两圆相交于点A、B，当MN⊥AB时，MN最长，过A任作一直线与⊙O₁交于M₁，与⊙O₂交于N₁，连接BM、BN、BM₁、BN₁，先证明△MBN∽△M₁BN₁，根据相似三角形性质，即可解决问题．

解答 解：结论：设两圆相交于点A、B，当MN⊥AB时，MN最长．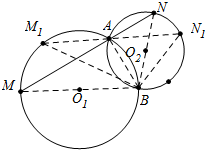
过A任作一直线与⊙O₁交于M₁，与⊙O₂交于N₁，连接BM、BN、BM₁、BN₁，
∵∠M=∠M₁，∠N=∠N₁，
∴△MBN∽△M₁BN₁，
∴$\frac{MN}{{M}_{1}{N}_{1}}$=$\frac{BN}{B{N}_{1}}$，
∴BN最大时，MN最大，
∴当BN是直径时，MN最大，
∴∠BAN=90°，
∴MN⊥AB时，MN最长．

点评 本题考查相交两个圆的性质，相似三角形的判定和性质等知识，解题的关键是添加辅助线，构造相似三角形，利用直径是最长的弦解决问题．