题目内容
14．一个盒子里装有除颜色外其余都相同的3个红球和2个白球，从中随机摸出一个球，记下颜色后放回，搅匀后，再摸第二个球，请利用画树状图或列表格的方法，求两次摸到的球的颜色相同的概率．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸到的球的颜色相同的情况，再利用概率公式求解即可求得答案．
解答 解：画树状图得：
∵共有25种等可能的结果，两次摸到的球的颜色相同的有13种情况，
∴两次摸到的球的颜色相同的概率为：$\frac{13}{25}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
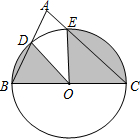如图，以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E．若∠A=80°，BC=4，则图中阴影部分图形的面积和为（ ）
如图，以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E．若∠A=80°，BC=4，则图中阴影部分图形的面积和为（ ）| A． | $\frac{64}{9}π$ | B． | $\frac{32}{9}π$ | C． | $\frac{16}{9}π$ | D． | $\frac{8}{9}π$ |
5．
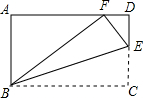如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（ ）
如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{5}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
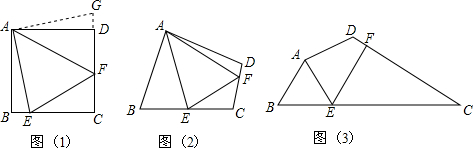
如图，给一幅长8m，宽5m的矩形风景画（图中阴影部分）镶一个画框，若设画框的宽均为xm，装好画框后总面积为70m2，则根据题意可列方程为（8+2x）（5+2x）=70．
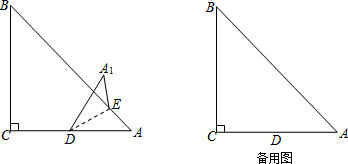
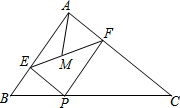如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是$\frac{12}{5}$．
3．下列各式计算正确的是（ ）
| A． | a3+a4=a7 | B． | （3a+b）2=9a2+b2 | C． | （-ab3）2=a2b6 | D． | a6b÷a2=a3b |
