题目内容
6.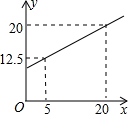 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( )
若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( )| A. | 7cm | B. | 8.5cm | C. | 9cm | D. | 10cm |
分析 先根据函数图象运用待定系数法求出函数的解析式,当x=0时代入解析式就可与y的值而得出结论.
解答 解:设函数的解析式为y=kx+b,由函数图象得
$\left\{\begin{array}{l}{12.5=5k+b}\\{20=20k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=10}\end{array}\right.$,
∴y=$\frac{1}{2}$x+10.
当x=0时,y=10.
故选:D.
点评 本题考查了待定系数法求一次函数的解析式的运用,由自变量的值求函数的解析式的运用,解答本题时求出解析式是关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
1.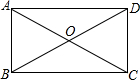 如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
 如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 8 |
15.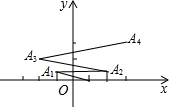 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )| A. | (50,49) | B. | (51,50) | C. | (-50,49) | D. | (100,99) |
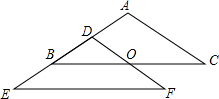 如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.
如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.