题目内容
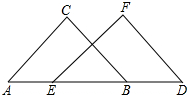 如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.
如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.考点:全等三角形的判定
专题:
分析:由AE=BD,则可得AB=DE,又由AC∥DF,得∠A=∠FED,已知∠C=∠F,易证△ABC≌△EDF(AAS),所以∠CBA=∠FED,即可证得BC∥DF.
解答:解:BC∥DF.
理由如下:
∵AC∥EF,
∴∠A=∠FED(两直线平行,同位角相等).
∵AE=BD,
∴AE+EB=EB+BD,即得AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(AAS),
∴∠CBA=∠FDF,
∴BC∥DF.
理由如下:
∵AC∥EF,
∴∠A=∠FED(两直线平行,同位角相等).
∵AE=BD,
∴AE+EB=EB+BD,即得AB=ED,
在△ABC和△EDF中,
|
∴△ABC≌△EDF(AAS),
∴∠CBA=∠FDF,
∴BC∥DF.
点评:本题主要考查了全等三角形的判定与性质和平行线的判定,学生应熟练掌握证明三角形全等的几个判定定理及其性质.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 2011年,在长沙创建全国文明城市过程中,某学校数学兴趣小组对全校1500名学生中的部分学生进行了“垃圾分类知识”的抽样测试调查,测试问卷采用等级计分.该兴趣小组把收集到的数据统计成以下表格.
2011年,在长沙创建全国文明城市过程中,某学校数学兴趣小组对全校1500名学生中的部分学生进行了“垃圾分类知识”的抽样测试调查,测试问卷采用等级计分.该兴趣小组把收集到的数据统计成以下表格.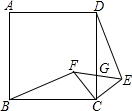 如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
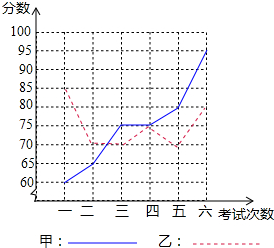 甲、乙两名同学进入初四后,某科6次考试成绩如图:
甲、乙两名同学进入初四后,某科6次考试成绩如图: