题目内容
关于x、y的多项式6mx2+4nxy+2x+2xy-x2+y+4不含二次项,求6m-2n-2的值.
考点:多项式
专题:
分析:由于多项式6mx2+4nxy+2x+2xy-x2+y+4不含二次项,即二次项系数为0,在合并同类项时,可以得到二次项为0,6m2-x2=0,4n+2=0,解方程即可求出n,m,然后把m、n的值代入6m-2n-2,即可求出代数式的值.
解答:解:6mx2+4nxy+2x+2xy-x2+y+4=(6m-1)x2+(4n+2)xy+2x+y+4,
∵它不含二次项,
∴6m-1=0,且4n+2=0,
∴m=
,n=-
,
∴6m-2n-2=6×
+2×
-2=0.
∵它不含二次项,
∴6m-1=0,且4n+2=0,
∴m=
| 1 |
| 6 |
| 1 |
| 2 |
∴6m-2n-2=6×
| 1 |
| 6 |
| 1 |
| 2 |
点评:此题考查了多项式,根据在多项式中不含哪一项,则哪一项的系数为0,由此建立方程,解方程即可求得待定系数的值.

练习册系列答案
相关题目
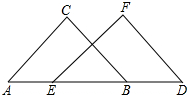 如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.
如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.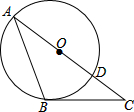 如图,△ABC中,BC=2,∠C=2∠A=45°,在AC边上取一点O,以点O为圆心,OA为半径的圆与AC边相交于点D,⊙O经过点B.
如图,△ABC中,BC=2,∠C=2∠A=45°,在AC边上取一点O,以点O为圆心,OA为半径的圆与AC边相交于点D,⊙O经过点B.