题目内容
11.若点(x1,y1),(x2,y2)都是反比例函数y=-$\frac{1}{x}$图象上的点,并且y1<0<y2,则下列结论中正确的是( )| A. | x1<x2 | B. | x2<x1 | ||
| C. | y随x的增大而增大 | D. | 两点有可能在同一象限 |
分析 根据函数的解析式得出反比例函数y=-$\frac{1}{x}$的图象在第二、四象限,求出点(x1,y1)在第四象限的图象上,点(x2,y2)在第二象限的图象上,再逐个判断即可.
解答 解:反比例函数y=-$\frac{1}{x}$的图象在第二、四象限,
∵y1<0<y2,
∴点(x1,y1)在第四象限的图象上,点(x2,y2)在第二象限的图象上,
∴x2<x1,
A、x2<x1,故本选项错误;
B、x2<x1,故本选项正确;
C、在每一个象限内,y随x的增大而增大,故本选项错误;
D、点(x1,y1)在第四象限的图象上,点(x2,y2)在第二象限的图象上,故本选项错误;
故选B.
点评 本题考查了反比例函数的图象和性质的应用,能熟记反比例函数的性质是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.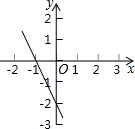 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
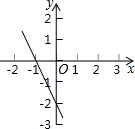 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
20.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点坐标为( )
| A. | (2,-3) | B. | (3,2) | C. | (-2,3) | D. | (-2,-3) |
 如图,反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A,B,它们的横坐标分别为1,3,则△OAB的面积为8.
如图,反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A,B,它们的横坐标分别为1,3,则△OAB的面积为8. 如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).
如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).
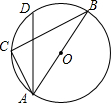 如图,△ABC内接于⊙O,AB为O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=3,则AC=$\sqrt{3}$.
如图,△ABC内接于⊙O,AB为O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=3,则AC=$\sqrt{3}$.