题目内容
17．
如图，在△ABC中，点D是BC的中点，点E、F分别在线段AD及其延长线上，且DE=DF．下列条件使四边形BECF为菱形的是（ ）| A． | BE⊥CE | B． | BF∥CE | C． | BE=CF | D． | AB=AC |
分析 根据等腰三角形的性质和已知求出EF⊥BC，BD=DC，先根据平行四边形的判定得出四边形BECF是平行四边形，再根据菱形的判定推出即可．
解答 解：条件是AB=AC，
理由是：∵AB=AC，点D是BC的中点，
∴EF⊥BC，BD=DC，
∵DE=DF，
∴四边形BECF是平行四边形，
∵EF⊥BC，
∴四边形BECF是菱形，
选项A、B、C的条件都不能推出四边形BECF是菱形，
即只有选项D正确，选项A、B、C都错误；
故选D．
点评 本题考查了等腰三角形的性质，平行四边形的判定，菱形的判定的应用，能熟记菱形的判定定理是解此题的关键，注意：对角线相等的平行四边形是菱形．
练习册系列答案
相关题目
在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点．且规定，正方形的内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点，…，则边长为8的正方形内部的整点的个数为49．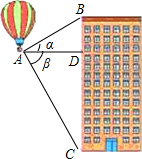
热气球的探测器显示，从热气球看一栋楼顶部的仰角α为27°，看这栋楼底部的俯角β为58°，热气球与这栋楼的水平距离为120米，这栋楼有多高（结果取整数）？
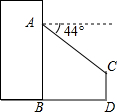如图，李明在自家楼房的窗口A处，测量楼前的路灯CD的高度，现测得窗口处A到路灯顶部C的仰角为44°，到地面的距离AB为20米，楼底到路灯的距离BD为12米，求路灯CD的高度（结果精确到0.1）
如图，反比例函数y=$\frac{6}{x}$在一象限的图象上有两点A，B，它们的横坐标分别为1，3，则△OAB的面积为8．
在平面直角坐标xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．
如图，二次函数y=ax2-4ax+2的图象与y轴交于点A，且过点B（3，6）．