题目内容
已知在平面直角坐标系内有一直线l:(2m+1)x+(m+1)y=7m+4.
(1)若不论m为何值,直线l都经过一定点,试求这个定点的坐标;
(2)若以A(1,2)为圆心,3为半径画⊙A,求⊙A被直线l截得的最短弦长.
(1)若不论m为何值,直线l都经过一定点,试求这个定点的坐标;
(2)若以A(1,2)为圆心,3为半径画⊙A,求⊙A被直线l截得的最短弦长.
考点:垂径定理,一次函数图象上点的坐标特征,勾股定理
专题:
分析:(1)直线方程即 m(2x+y-7)+(x+y-4)=0,一定经过2x+y-7=0和x+y-7=0 的交点,联立方程组可求定点的坐标;
(2)设定点为P(3,1),由于经过P点的直线l⊥AP时⊙A被直线l截得的弦最短,先求得AP,再根据勾股定理求得PC,进而求得弦BC的长,即可求得⊙A被直线l截得的最短弦长.
(2)设定点为P(3,1),由于经过P点的直线l⊥AP时⊙A被直线l截得的弦最短,先求得AP,再根据勾股定理求得PC,进而求得弦BC的长,即可求得⊙A被直线l截得的最短弦长.
解答:解:(1)直线:(2m+1)x+(m+1)y=7m+4.
即 m(2x+y-7)+(x+y-4)=0,
根m的任意性可得
,
解得
,
∴不论m为何值,直线l都经过一定点(3,1).
(2)设定点为P(3,1),
∵经过P点的直线l⊥AP时⊙A被直线l截得的弦最短,
∵A(1,2),P(3,1),
∴AP=
=
,
∵AC=3,
∴PC=
=2
∴BC=2PC=4,
∴⊙A被直线l截得的最短弦长为4.
即 m(2x+y-7)+(x+y-4)=0,
根m的任意性可得
|
解得
|
∴不论m为何值,直线l都经过一定点(3,1).
(2)设定点为P(3,1),

∵经过P点的直线l⊥AP时⊙A被直线l截得的弦最短,
∵A(1,2),P(3,1),
∴AP=
| 11+22 |
| 5 |
∵AC=3,
∴PC=
| AC2-AP2 |
∴BC=2PC=4,
∴⊙A被直线l截得的最短弦长为4.
点评:本题考查经过两直线交点的直线系方程形式,直线与圆的位置关系,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知点(3-2k2,4k-3)在第一象限的角平分线上,则k=( )
| A、1 | B、-1 | C、0 | D、0或1 |
 如图,已知在等边△ABC,点D是△ABC角平分线AD、CD的交点,P为△ABC外一点上,∠APC=60°,连接DP.求证:PD平分∠APC.
如图,已知在等边△ABC,点D是△ABC角平分线AD、CD的交点,P为△ABC外一点上,∠APC=60°,连接DP.求证:PD平分∠APC.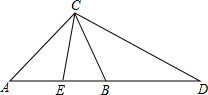 如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.
如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.