题目内容
已知一抛物线与x轴交于A(-2,0)、B(4,0),与y轴交于点C(0,-8),抛物线的顶点为M,求四边形ABMC的面积.
考点:抛物线与x轴的交点
专题:
分析:已知三点的坐标,可用交点式求二次函数解析式,然后将C点的坐标代入抛物线中,即可求出抛物线的解析式;由此得出M的坐标(可用配方法进行求解),进而将四边形ABMC分成梯形和两个直角三角形三部分来求.
解答:解:由题意,可设抛物线的解析式为y=a(x-4)(x+2).
将C点坐标代入后可得:
-8=a(0+2)(0-4),
即a=1,
因此抛物线的解析式为:y=(x+2)(x-4)=x2-2x-8,
=(x-1)2-9,
所以顶点M的坐标为:M(1,4),
过M作MN⊥x轴于N,
则有S四边形ABMC=S△AOC+S△BMN+S梯形MNOC
=
OA•OC+•
BN•MN+
(OC+MN)•ON=29.
将C点坐标代入后可得:
-8=a(0+2)(0-4),
即a=1,
因此抛物线的解析式为:y=(x+2)(x-4)=x2-2x-8,
=(x-1)2-9,
所以顶点M的坐标为:M(1,4),
过M作MN⊥x轴于N,
则有S四边形ABMC=S△AOC+S△BMN+S梯形MNOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了待定系数法求二次函数解析式以及图形面积的求法.当图形的形状不规则时,可将图形分割成几个规则图形,然后利用这些图形的面积的“和,差”关系来求解.

练习册系列答案
相关题目
 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
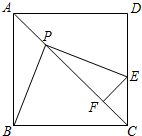 已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.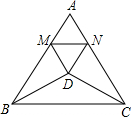 如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点做一个60°的∠MDN,点M、N分别在AB、AC上,求△AMN的周长.
如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点做一个60°的∠MDN,点M、N分别在AB、AC上,求△AMN的周长.