题目内容
 如图,已知在等边△ABC,点D是△ABC角平分线AD、CD的交点,P为△ABC外一点上,∠APC=60°,连接DP.求证:PD平分∠APC.
如图,已知在等边△ABC,点D是△ABC角平分线AD、CD的交点,P为△ABC外一点上,∠APC=60°,连接DP.求证:PD平分∠APC.考点:圆周角定理
专题:证明题
分析:连接AD,DC,由点D为△ABC的角平分线的交点,得出∠ADC=120°,又∠APC=60°,得出四边形ADCP外接一个圆.利用同弧所对的圆周角相等,即可得出DP平分∠APC.
解答:解:如图所示:连接AD,DC,

∵点D为△ABC的角平分线的交点,
∴∠ADC=120°,
又∵∠APC=60°,
∴四边形ADCP外接一个圆.
∵△ABC是等边三角形,点D是△ABC角平分线AD、CD的交点,
∴∠DAC=∠DPC=30°,
∴∠DCA=∠DPA=30°(同弧所对的圆周角相等),
∴DP平分∠APC.

∵点D为△ABC的角平分线的交点,
∴∠ADC=120°,
又∵∠APC=60°,
∴四边形ADCP外接一个圆.
∵△ABC是等边三角形,点D是△ABC角平分线AD、CD的交点,
∴∠DAC=∠DPC=30°,
∴∠DCA=∠DPA=30°(同弧所对的圆周角相等),
∴DP平分∠APC.
点评:本题主要考查了圆周角定理,解题的关键是确定四边形ADCP外接一个圆.

练习册系列答案
相关题目
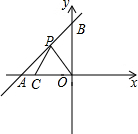 如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).
如图,直线l:y=kx+6分别与x轴、y轴交于点A、B,点A(-8,0),C为x轴上一点,且C的坐标为(-6,0).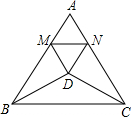 如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点做一个60°的∠MDN,点M、N分别在AB、AC上,求△AMN的周长.
如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点做一个60°的∠MDN,点M、N分别在AB、AC上,求△AMN的周长.