题目内容
15.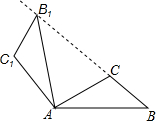 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )| A. | 70° | B. | 80° | C. | 84° | D. | 86° |
分析 由旋转的性质可知∠B=∠AB1C1,AB=AB1,由等腰三角形的性质和三角形的内角和定理可求得∠B=∠BB1A=∠AB1C1=40°,从而可求得∠BB1C1=80°.
解答 解:由旋转的性质可知:∠B=∠AB1C1,AB=AB1,∠BAB1=100°.
∵AB=AB1,∠BAB1=100°,
∴∠B=∠BB1A=40°.
∴∠AB1C1=40°.
∴∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°.
故选B.
点评 本题主要考查的是旋转的性质,由旋转的性质得到△ABB1为等腰三角形是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
20.下列计算正确的是( )
| A. | -a6•(-a)3=a8 | B. | (-3m-1)(3m-1)=-9m2+1 | ||
| C. | (x-2y)2=x2-4y2 | D. | [(-2x)2]3=-64x6 |
20.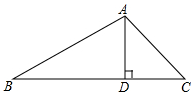 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{3}$ | D. | 15 |
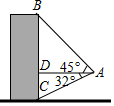 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的仰角为32°,已知该建筑物高BC为208米,求此时航拍无人机与该建筑物的水平距离AD(精确到0.1米)
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的仰角为32°,已知该建筑物高BC为208米,求此时航拍无人机与该建筑物的水平距离AD(精确到0.1米)
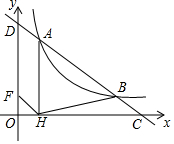 如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.
如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3. 如图,将Rt△ABC绕点C顺时针旋转90°得到△DCE,连接AE,若∠AED=10°,则∠B的度数为55°.
如图,将Rt△ABC绕点C顺时针旋转90°得到△DCE,连接AE,若∠AED=10°,则∠B的度数为55°.