题目内容
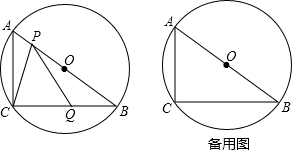
5. 如图,将Rt△ABC绕点C顺时针旋转90°得到△DCE,连接AE,若∠AED=10°,则∠B的度数为55°.
如图,将Rt△ABC绕点C顺时针旋转90°得到△DCE,连接AE,若∠AED=10°,则∠B的度数为55°.
分析 根据旋转的性质可得AC=EC,然后判断出△ACE是等腰直角三角形,根据等腰直角三角形的性质可得∠CAE=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CDE,然后根据旋转的性质可得∠B=∠CDE.
解答 解:∵将Rt△ABC绕点C顺时针旋转90°得到△DCE,
∴AC=AE,
∴△ACE是等腰直角三角形,
∴∠CAE=45°,
∴∠CDE=∠AED+∠CAE=10°+45°=55°,
由旋转的性质得∠B=∠CDE=55°.
故答案为:55.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
15.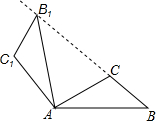 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )| A. | 70° | B. | 80° | C. | 84° | D. | 86° |
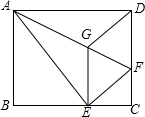 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
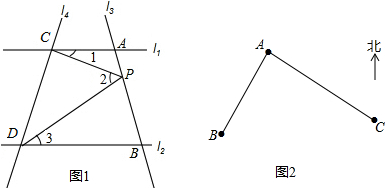
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG. 如图,BC⊥AB,DE⊥AB,DF∥BG,由此可判断∠1=∠2,请说明理由.
如图,BC⊥AB,DE⊥AB,DF∥BG,由此可判断∠1=∠2,请说明理由.