题目内容
10.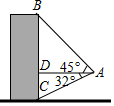 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的仰角为32°,已知该建筑物高BC为208米,求此时航拍无人机与该建筑物的水平距离AD(精确到0.1米)
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的仰角为32°,已知该建筑物高BC为208米,求此时航拍无人机与该建筑物的水平距离AD(精确到0.1米)【参考数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249】
分析 在首先证明△ABD是的等腰直角三角形,则BD=AD,然后在直角△ACD中,利用tan∠CAD=$\frac{CD}{AD}$,即可得到关于AD的方程,解方程求得AD的长.
解答 解:∵∠DAB=45°,AD⊥BC,
∴∠B=45°,
∴∠B=∠BAD,
∴BD=AD.
∴CD=208-AD.
在Rt△ADC中,∠ADC=90°,
tan∠CAD=$\frac{CD}{AD}$,
∴AD•tan32°=CD,
∴0.6249AD=208-AD,
∴AD≈128.0.
答:此时航拍无人机与该建筑物的水平距离AD约是128.0米.
点评 此题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
15. 已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )
已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )
 已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )
已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )| A. | (1,4) | B. | (1,5) | C. | (2,3) | D. | (2,4) |
15.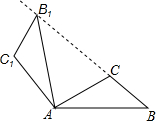 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )| A. | 70° | B. | 80° | C. | 84° | D. | 86° |
2.将二次函数y=-(x-2)2-3的图象先向右平移2个单位,再向上平移2单位后,所得图象的函数表达式是( )
| A. | y=-x2-1 | B. | y=-x2-5 | C. | y=-(x-4)2-1 | D. | y=-(x-4)2-5 |
19.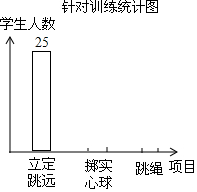 中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
针对性训练统计表
(1)请将统计表、统计图补充完整;
(2)请以小明的统计结果来估算该校九年级480名学生参加“跳绳”训练的人数.
 中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.针对性训练统计表
| 项目 | 频数 | 百分比 |
| 立定跳远 | 25 | |
| 掷实心球 | 20% | |
| 跳绳 | ||
| 合计 | 50 | 1 |
(2)请以小明的统计结果来估算该校九年级480名学生参加“跳绳”训练的人数.
 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. 如图,一棵树高9米,被大风刮断,树尖着地点B距树底部C为3米,求折断点A离地高度多少米?
如图,一棵树高9米,被大风刮断,树尖着地点B距树底部C为3米,求折断点A离地高度多少米?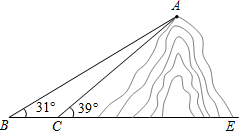 如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).
如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).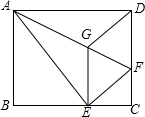 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.