题目内容
4.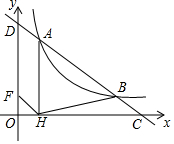 如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.
如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.
分析 解:设 OH=a 则 HC=5a,把C(6a,0)代入 y=-$\frac{1}{2}$x+m 得m=3a,设A点坐标为 (a,n) 代入 y=-$\frac{1}{2}$x+m 得到A(a,$\frac{5}{2}$a) 代入 y=$\frac{k}{x}$得 $\frac{5}{2}$a=$\frac{k}{a}$求得k=$\frac{5}{2}$a2,于是得到H点坐标为(a,$\frac{5}{2}$a) B点坐标为(5a,$\frac{1}{2}$a2)根据三角形的面积列方程即可得到结论.
解答 解:设 OH=a 则 HC=5a,
∴C(6a,0)代入 y=-$\frac{1}{2}$x+m 得 m=3a,
m=3a,
设A点坐标为 (a,n) 代入 y=-$\frac{1}{2}$x+m 得 n=-$\frac{1}{2}$a+3a
n=$\frac{5}{2}$a,
∴A(a,$\frac{5}{2}$a) 代入 y=$\frac{k}{x}$得 $\frac{5}{2}$a=$\frac{k}{a}$,
∴k=$\frac{5}{2}$a2,
∴y=-$\frac{1}{2}$x+3a ①
y=$\frac{5{a}^{2}}{2x}$ ②
由①②得-$\frac{1}{2}$ x+3a=$\frac{5{a}^{2}}{2x}$,
化简,得 x2-6ax+5a2=0,
解得:x=5a 或 x=a,
∴A点坐标为(a,$\frac{5}{2}$a) B点坐标为(5a,$\frac{1}{2}$a)
∴△ABH的底边=AH=$\frac{5}{2}$a,△ABH的高=B点横坐标-H点横坐标=5a-a=4a,
∴S△ABH=$\frac{1}{2}$×△ABH的底边×△ABH的高=$\frac{1}{2}×$$\frac{5}{2}$a×4a=5a2 ③
∵S△ABH=6,④
由③④得 5a2=6,
∴k=$\frac{5}{2}$a2=3.
点评 本题考查了一次函数与反比例函数的交点问题,待定系数法求函数的解析式,三角形面积的计算,正确的理解题意是解题的关键.

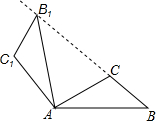 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )| A. | 70° | B. | 80° | C. | 84° | D. | 86° |
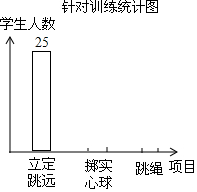 中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.针对性训练统计表
| 项目 | 频数 | 百分比 |
| 立定跳远 | 25 | |
| 掷实心球 | 20% | |
| 跳绳 | ||
| 合计 | 50 | 1 |
(2)请以小明的统计结果来估算该校九年级480名学生参加“跳绳”训练的人数.
 如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)