题目内容
20.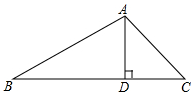 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{3}$ | D. | 15 |
分析 根据垂直可得∠ADB=∠ADC,然后在Rt△ACD中,利用∠DAC的余弦求出AD的长度,在Rt△ABD中,利用∠B的正弦求出AB的长度,再根据勾股定理列式求解即可得到BD的长短.
解答 解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ACD中,∵∠DAC=45°,AC=10$\sqrt{2}$,
∴AD=AC•cos45°=10$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=10,
在Rt△ABD中,∵sin∠B=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴AB=2AD=2×10=20,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{2{0}^{2}-1{0}^{2}}$=10$\sqrt{3}$.
故选C.
点评 本题考查了解直角三角形,勾股定理的应用,根据垂直得到直角三角形是解题的关键,解决此类题目要熟练掌握特殊角的三角函数值.

练习册系列答案
相关题目
15.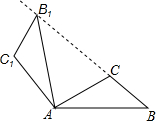 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )| A. | 70° | B. | 80° | C. | 84° | D. | 86° |
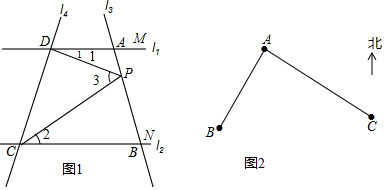
 如图,AB∥CD,∠1=130°,∠2=85°,则∠3=45°.
如图,AB∥CD,∠1=130°,∠2=85°,则∠3=45°. 如图,AB∥CD,直线l交AB于点E,交CD于点F,FG平分∠EFD交直线AB于点G.求证:△EFG是等腰三角形.
如图,AB∥CD,直线l交AB于点E,交CD于点F,FG平分∠EFD交直线AB于点G.求证:△EFG是等腰三角形. 如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)