题目内容
15.函数$\frac{1}{2}$≤x≤2时,$\frac{1}{4}$≤y≤1,则这个函数可以是( )| A. | y=$\frac{1}{2x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{1}{8x}$ | D. | y=$\frac{8}{x}$ |
分析 把x=$\frac{1}{2}$代入四个选项中的解析式可得y的值,再把x=2代入解析式可得y的值,然后可得答案.
解答 解:A、把x=$\frac{1}{2}$代入y=$\frac{1}{2x}$可得y=1,把x=2代入y=$\frac{1}{2x}$可得y=$\frac{1}{4}$,故A正确;
B、把x=$\frac{1}{2}$代入y=$\frac{2}{x}$可得y=4,把x=2代入y=$\frac{2}{x}$可得y=1,故B错误;
C、把x=$\frac{1}{2}$代入y=$\frac{1}{8x}$可得y=$\frac{1}{4}$,把x=2代入y=$\frac{1}{8x}$可得y=$\frac{1}{16}$,故C错误;
D、把x=$\frac{1}{2}$代入y=$\frac{8}{x}$可得y=16,把x=2代入y=$\frac{8}{x}$可得y=4,故D错误.
故选:A.
点评 此题主要考查了反比例函数图象的性质,关键是正确理解题意,根据自变量的值求出对应的函数值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列从左到右的变形是因式分解的是( )
| A. | (x-4)(x+4)=x2-16 | B. | x2-y2+2=(x+y)(x-y)+2 | ||
| C. | x2+1=x(x+$\frac{1}{x}$) | D. | a2b+ab2=ab(a+b) |
7.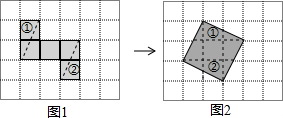 如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
 如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
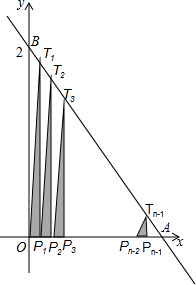 如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{1007}{2015}$.
如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{1007}{2015}$. 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.