题目内容
10.已知点P是反比例函数y=$\frac{4}{x}$图象上的一个动点,在y轴上取点Q,使得△OPQ为等腰直角三角形,则符合条件的Q点的坐标为(0,2)、(0,-2)、(0,4)或(0,-4).分析 根据题意,分两种情况:(1)当∠AQP=90°时;(2)当∠APQ=90°时;根据△OPQ为等腰直角三角形,判断出符合条件的所有Q点的坐标有哪些即可.
解答 解:(1)当∠AQP=90°时,
∵△OPQ为等腰直角三角形,
∴OQ=PQ,
∴点P(a,b)的横坐标、纵坐标相等,
∴a=b,ab=4,
解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{b=-2}\end{array}\right.$
∴Q点的坐标为(0,2)或(0,-2).
(2)当∠APQ=90°时,
∵△OPQ为等腰直角三角形,
∴OP=PQ,
∴点P(a,b)的横坐标、纵坐标相等,
∴a=b,ab=4,
解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{b=-2}\end{array}\right.$
∴OP=$\sqrt{{2}^{2}{+2}^{2}}=2\sqrt{2}$,PQ=2$\sqrt{2}$,
∵△OPQ为等腰直角三角形,
∴OQ=2$\sqrt{2}×\sqrt{2}$=4,
∴Q点的坐标为(0,4)或(0,-4).
综上,可得符合条件的Q点的坐标为:(0,2)、(0,-2)、(0,4)或(0,-4).
故答案为:(0,2)、(0,-2)、(0,4)或(0,-4).
点评 (1)此题主要考查了反比例函数图象上点的坐标的特征,要熟练掌握,解答此题的关键是要明确:①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
(2)此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径.

 阅读快车系列答案
阅读快车系列答案| A. | y=$\frac{1}{2x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{1}{8x}$ | D. | y=$\frac{8}{x}$ |
 如图,直线m∥n,BA⊥AC于A点,AB、AC分别交直线n于点B、C,∠2=55°,则∠1的度数是( )
如图,直线m∥n,BA⊥AC于A点,AB、AC分别交直线n于点B、C,∠2=55°,则∠1的度数是( )| A. | 50° | B. | 45° | C. | 35° | D. | 30° |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
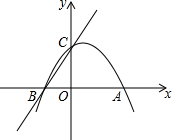 如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).
如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).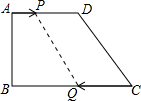 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.