题目内容
5.计算(1)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
(2)6-2$\sqrt{\frac{3}{2}}$-3$\sqrt{\frac{3}{2}}$
(3)(2$\sqrt{3}$+3$\sqrt{2}$)(2$\sqrt{3}$-3$\sqrt{2}$)
(4)($\sqrt{48}$+$\frac{1}{4}$$\sqrt{6}$)÷$\sqrt{27}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用平方差公式计算;
(4)先把各二次根式化为最简二次根式,然后进行二次根式的除法运算.
解答 解:(1)原式=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(2)原式=6-$\sqrt{6}$-$\frac{3\sqrt{6}}{2}$
=6-$\frac{5\sqrt{6}}{2}$;
(3)原式=12-18
=-6;
(4)原式=(4$\sqrt{3}$+$\frac{\sqrt{6}}{4}$)÷3$\sqrt{3}$
=$\frac{4}{3}$+$\frac{\sqrt{2}}{12}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
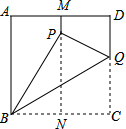 如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.
如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.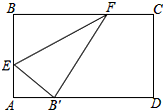 如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.
如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值. 已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式y1<y2的解集是x<1.
已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式y1<y2的解集是x<1.