题目内容
1.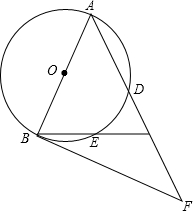 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.(1)试判断:直线BF与⊙O的位置关系,并说明理由;
(2)若AB=6,BF=8,求tan∠CBF.
分析 (1)连结AE,如图,根据圆周角定理得到∠AEB=90°,则利用等腰三角形的性质得AE平分∠BAC,即∠BAE=$\frac{1}{2}$∠BAC,加上∠CAB=2∠CBF,所以∠BAE=∠CBF,接着利用∠BAE+∠ABE=90°得到∠CBF+∠ABE=90°,然后根据切线的判定定理得到直线BF为⊙O的切线;
(2)作CH⊥BF于H,如图,先利用勾股定理计算出AF=10,则CF=AF-AC=AF-AB=4,再证明Rt△FCH∽Rt△FAB,利用相似比计算出CH=$\frac{12}{5}$,FH=$\frac{16}{5}$,则BH=BF-HF=$\frac{24}{5}$,
然后在Rt△CBH中根据正切的定义求解.
解答 解:(1)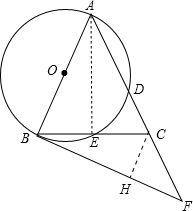 直线BF与⊙O相切.理由如下:
直线BF与⊙O相切.理由如下:
连结AE,如图,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC,
∵∠CAB=2∠CBF,
∴∠BAE=∠CBF,
而∠BAE+∠ABE=90°,
∴∠CBF+∠ABE=90°,即∠ABF=90°,
∴AB⊥BF,
∴直线BF为⊙O的切线;
(2)作CH⊥BF于H,如图,
在Rt△ABF中,∵AB=6,BF=8,
∴AF=10,
∴CF=AF-AC=AF-AB=10-6=4,
∵∠CFH=∠AFB,
∴Rt△FCH∽Rt△FAB,
∴$\frac{CH}{AB}$=$\frac{FH}{BF}$=$\frac{CF}{AF}$,即$\frac{CH}{6}$=$\frac{FH}{8}$=$\frac{4}{10}$,
∴CH=$\frac{12}{5}$,FH=$\frac{16}{5}$,
∴BH=BF-HF=8-$\frac{16}{5}$=$\frac{24}{5}$,
在Rt△CBH中,tan∠CBH=$\frac{CH}{BH}$=$\frac{\frac{12}{5}}{\frac{24}{5}}$=$\frac{1}{2}$,
即tan∠CBF=$\frac{1}{2}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

| A. | (-1)2005=-1 | B. | |-3|=±3 | C. | ${({\frac{1}{3}})^{-1}}$=3 | D. | -22=-4 |
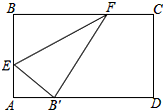 如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.
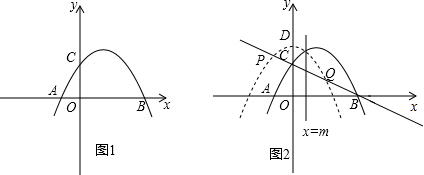
如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值. 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B. 已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式y1<y2的解集是x<1.
已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式y1<y2的解集是x<1. 已知:如图,?ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.
已知:如图,?ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.