题目内容
9.从方程到函数的变化:(1)若一元二次方程x2-(m+1)x+m=0的两个根为x1、x2.当x1+x2=3时,求m的值;
(2)若二次函数y=x2-(m+1)x+m的图象与x轴交于A、B两点,O为坐标原点,当OA+OB=3时,求m的值.
分析 (1)根据根与系数的关系即可得到x1+x2=m+1,则可以得到一个关于m的方程,求得m的值;
(2)当y=0时,x2-(m+1)x+m=0,求得方程的解,根据OA+OB=3,m即可求得.
解答 解:(1)根据题意得x1+x2=m+1=3,
解得:m=2;
(2)当y=0时,x2-(m+1)x+m=0,
解得:x1=1,x2=m.
∵OA+OB=3,
∴1+|m|=3,
解得:m=2或-2.
点评 本题考查了二次函数与一元二次方程的关系,正确利用根与系数的关系是关键.

练习册系列答案
相关题目
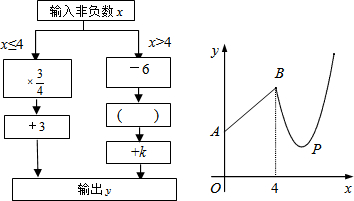
4.如图是数值转换机的示意图,小明按照其对应系画出了y与x的函数图象.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.

1.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2+1的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
19.关于函数y=-$\frac{1}{2}$x,下列结论正确的是( )
| A. | 函数图象必经过点(-1,2) | B. | 函数图象经过第二、四象限 | ||
| C. | y随x的增大而增大 | D. | 不论x取何值,总有y>0 |