题目内容
10.先化简,再求值:$\frac{{m}^{2}-4m+4}{{m}^{2}-1}$÷$\frac{m-2}{m-1}$+$\frac{2}{m-1}$,其中m=2.分析 首先利用分式的乘除运算法则化简进而将m=2代入求出即可.
解答 解:$\frac{{m}^{2}-4m+4}{{m}^{2}-1}$÷$\frac{m-2}{m-1}$+$\frac{2}{m-1}$
=$\frac{(m-2)^{2}}{(m-1)(m+1)}$×$\frac{m-1}{m-2}$+$\frac{2}{m-1}$
=$\frac{m-2}{m+1}$+$\frac{2}{m-1}$
=$\frac{(m-2)(m-1)}{(m+1)(m-1)}$+$\frac{2(m+1)}{(m+1)(m-1)}$
=$\frac{{m}^{2}-m+4}{(m+1)(m-1)}$,
将m=2代入上式得:
原式=$\frac{{2}^{2}-2+4}{(2+1)×(2-1)}$=-$\frac{3}{2}$.
点评 此题主要考查了分式的化简求值,正确分解因式进行分式混合运算是解题关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
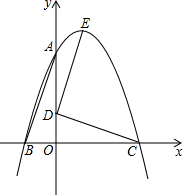 如图,直线y=3x+3与x轴、y轴分别交于点B、A,O为原点,△AOB绕点O顺时针方向旋转90°后得到△COD.
如图,直线y=3x+3与x轴、y轴分别交于点B、A,O为原点,△AOB绕点O顺时针方向旋转90°后得到△COD.