题目内容
10. 如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )
如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
分析 由△AFG∽△BFC,可确定结论①正确;由△AFG≌△AFD可得AG=$\frac{1}{2}$AB=$\frac{1}{2}$BC,进而由△AFG∽△BFC确定点F为AC的三等分点,可确定结论②正确;当B、C、F、D四点在同一个圆上时,由圆内接四边形的性质得到∠2=∠ACB由于∠ABC=90°,AB=BC,得到∠ACB=∠CAB=45°,于是得到∠CFD=∠AFD=90°,根据垂径定理得到DF=DB,故③正确;因为F为AC的三等分点,所以S△ABF=$\frac{1}{3}$S△ABC,又S△BDF=$\frac{1}{2}$S△ABF,所以S△ABC=6S△BDF,由此确定结论④错误.
解答 解:依题意可得BC∥AG,
∴△AFG∽△BFC,
∴$\frac{AG}{BC}=\frac{AF}{CF}$,
又AB=BC,∴$\frac{AG}{AB}=\frac{AF}{CF}$.
故结论①正确;
如右图,∵∠1+∠3=90°,∠1+∠4=90°,
∴∠3=∠4.
在△ABG与△BCD中,
$\left\{\begin{array}{l}{∠3=∠4}\\{AB=BC}\\{∠BAG=∠CBD=90°}\end{array}\right.$,
∴△ABG≌△BCD(ASA),
∴AG=BD,又BD=AD,
∴AG=AD;
在△AFG与△AFD中,$\left\{\begin{array}{l}{AG=AD}\\{∠FAD=∠FAG=45°}\\{AF=AF}\end{array}\right.$,
∴△AFG≌△AFD(SAS)
∵△ABC为等腰直角三角形,∴AC=$\sqrt{2}$AB;
∵△AFG≌△AFD,∴AG=AD=$\frac{1}{2}$AB=$\frac{1}{2}$BC;
∵△AFG∽△BFC,∴$\frac{AG}{BC}$=$\frac{AF}{FC}$,∴FC=2AF,
∴AF=$\frac{1}{3}$AC=$\frac{\sqrt{2}}{3}$AB.
故结论②正确;
当B、C、F、D四点在同一个圆上时,
∴∠2=∠ACB
∵∠ABC=90°,AB=BC,
∴∠ACB=∠CAB=45°,
∴∠2=45°,
∴∠CFD=∠AFD=90°,
∴CD是B、C、F、D四点所在圆的直径,
∵BG⊥CD,
∴$\widehat{DF}=\widehat{BD}$,
∴DF=DB,故③正确;
∵$\frac{AG}{AB}=\frac{AF}{CF}$,∵AG=BD,$\frac{BD}{AD}=\frac{1}{2}$,
∴$\frac{BD}{AB}=\frac{1}{3}$,∴$\frac{AF}{CF}$=$\frac{1}{3}$,∴AF=$\frac{1}{4}$AC,∴S△ABF=$\frac{1}{4}$S△ABC;∴S△BDF=$\frac{1}{3}$S△ABF,
∴S△BDF=$\frac{1}{12}$S△ABC,即S△ABC=12S△BDF.
故结论④错误.
故选C.
点评 本题考查了等腰直角三角形中相似三角形与全等三角形的应用,有一定的难度.对每一个结论,需要仔细分析,严格论证;注意各结论之间并非彼此孤立,而是往往存在逻辑关联关系,需要善加利用.

 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
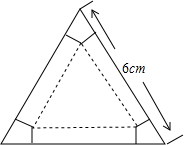 如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )| A. | $\sqrt{3}$cm2 | B. | $\frac{3}{2}$$\sqrt{3}$cm2 | C. | $\frac{9}{2}$$\sqrt{3}$cm2 | D. | $\frac{27}{2}$$\sqrt{3}$cm2 |
 如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )| A. | 转化思想 | |
| B. | 三角形的两边之和大于第三边 | |
| C. | 两点之间,线段最短 | |
| D. | 三角形的一个外角大于与它不相邻的任意一个内角 |

 如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,则$\frac{1}{AM}$+$\frac{1}{AN}$=1.
如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,则$\frac{1}{AM}$+$\frac{1}{AN}$=1.


