题目内容
20. 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
分析 先由平行线证明△ADE∽△ABC,得出对应边成比例$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{2}{5}$,即可得出$\frac{AD}{DB}$的值.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{2}{5}$,
∴$\frac{AD}{DB}=\frac{2}{3}$;
故选:B.
点评 本题考查了相似三角形的判定与性质、比例的性质;熟练掌握相似三角形的判定与性质是解决问题的关键

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10. 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
 如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )
如图,⊙O的直径CD⊥AB,∠CDB=25°,则∠AOC的度数为( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
11.在△ABC中,∠C=90°,sinA=$\frac{3}{5}$,D是AB的中点,则tan∠BCD+tan∠ACD=( )
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
8.若x=-$\frac{1}{3}$,则|x|的值是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
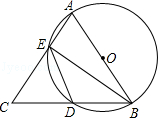 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE. 在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A(4,0)和B(0,2)
在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A(4,0)和B(0,2)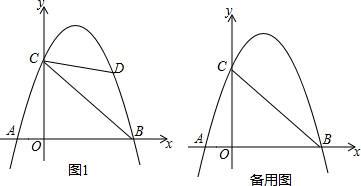
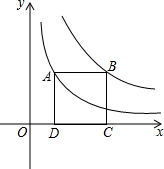 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{6}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD为正方形,则AB=2.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双曲线y=$\frac{6}{x}$上,且AB∥x轴,C、D在x轴上,若四边形ABCD为正方形,则AB=2. 如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )
如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )