题目内容
9.已知3|a+2b-1|+8(b+1)2=0,x=-2是方程k(x-2)=3x-k的根,且代数式$\frac{kb-a+m}{2}$的值比$\frac{b}{k}$-a+m的值大2,求m的值.分析 首先根据非负数的性质即可列方程组求得a和b的值,把x=-2代入方程k(x-2)=3x-k的根,求的k的值,然后根据代数式$\frac{kb-a+m}{2}$的值比$\frac{b}{k}$-a+m的值大2即可列方程求得m的值.
解答 解:根据题意得:$\left\{\begin{array}{l}{a+2b-1=0}\\{b+1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=-1}\end{array}\right.$.
把x=-2代入k(x-2)=3x-k得:-4k=-6-k,
解得:k=2.
则$\frac{-2-3+m}{2}$-(-$\frac{1}{2}$-3+m)=2,
解得:m=-2.
点评 本题考查了非负数的性质以及方程的解的定义,方程的解就是能使方程左右两边相等的未知数的值,求得a、b、k的值是关键.

练习册系列答案
相关题目
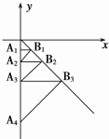 如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,再过点A2作y轴的垂线,交直线y=-x于点B2…则点B4的坐标为($\frac{8}{3}$,-$\frac{8}{3}$).
如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,再过点A2作y轴的垂线,交直线y=-x于点B2…则点B4的坐标为($\frac{8}{3}$,-$\frac{8}{3}$).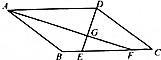 如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明.
如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明.