题目内容
17.已知一次函数y=-$\frac{4}{3}$x+4与x轴,y轴分别交于M,N两点.(1)求△OMN的面积;
(2)若OC⊥MN于点C,求OC的长;
(3)若点P是直线上一动点,且△OPM的面积为3,直接写出满足条件的所有点P的坐标.
分析 (1)分别令一次函数y=-$\frac{4}{3}$x+4中的x、y为0,即可得出点M、N的坐标,即得出线段OM、ON的长度,结合三角形的面积公式即可得出结论;
(2)在直角三角形中依据勾股定理即可得出线段MN的长度,再结合三角形的面积公式即可求出底边MN上的高OC的长度;
(3)依据点P在直线上,设出点P的坐标,结合三角形的面积公式即可得出点P的纵坐标,将其代入点P的坐标中,即可得出结论.
解答 解:(1)依据题意画出图形,如图1所示.
令一次函数y=-$\frac{4}{3}$x+4中x=0,则y=4;
令一次函数y=-$\frac{4}{3}$x+4中y=0,则-$\frac{4}{3}$x+4=0,解得x=3.
∴点M(3,0),点N(0,4),
∴OM=3,ON=4.
S△OMN=$\frac{1}{2}$OM•ON=$\frac{1}{2}$×3×4=6.
(2)在Rt△OMN中,∠MON=90°,OM=3,ON=4,
∴MN=$\sqrt{O{M}^{2}+O{N}^{2}}$=5.
∵S△OMN=$\frac{1}{2}$MN•OC=6,
∴OC=$\frac{12}{5}$.
(3)设点P的坐标为(m,-$\frac{4}{3}$m+4),
∵△OPM的面积为3,且S△OPM=$\frac{1}{2}$OM•|-$\frac{4}{3}$m+4|,
∴|-$\frac{4}{3}$m+4|=2,
解得:m=$\frac{3}{2}$,或m=$\frac{9}{2}$.
故点P的坐标为($\frac{3}{2}$,2)或($\frac{9}{2}$,-2).
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积公式以及勾股定理,解题的关键是:(1)求出点M、N的坐标;(2)求出线段MN的长度;(3)根据三角形的面积公式得出关于点P纵坐标的方程.本题属于基础题,难度不大,解决该题型题目时,根据三角形的面积公式找出关于点的坐标的方程是关键.

| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
 如图,直线y=-$\frac{1}{2}$x+b与x轴、y轴分别交于点A、B,若点P(2,3)在△AOB内部,则b的可能值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴、y轴分别交于点A、B,若点P(2,3)在△AOB内部,则b的可能值是( )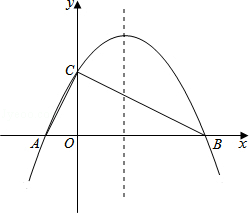 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(-2,0).