Question

1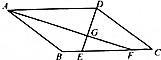．如图，四边形ABCD中，AD∥BC，AF，DE分别平分∠BAD和∠ADC，AF与DE相交于点G，AF⊥DE．判断四边形ABCD的形状，并证明．

Answer 1

分析 直接利用角平分线的性质结合AF⊥DE得出∠BAD+∠ADC=180°，即可得出AB∥CD，再利用平行四边形的判定方法得出答案．

解答 解：四边形ABCD是平行四边形，
∵AF，DE分别平分∠BAD和∠ADC，
∴∠DAF=$\frac{1}{2}$∠BAD，∠ADE=$\frac{1}{2}$∠ADC，
∵AF⊥DE，
∴∠AGD=90°，
∴∠DAF+∠ADE=90°，
∴$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠ADC=90°，
∴∠BAD+∠ADC=180°，
∴AB∥CD，
又∵AD∥BC，
∴四边形ABCD是平行四边形．

点评 此题主要考查了平行四边形的判定以及角平分线的定义，正确得出∠BAD+∠ADC=180°是解题关键．