Question

15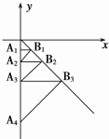．如图，在平面直角坐标系中，过点A₁（0，-$\frac{1}{3}$）作y轴的垂线，交直线y=-x于点B₁，再过点B₁作直线y=-x的垂线，交y轴于点A₂，再过点A₂作y轴的垂线，交直线y=-x于点B₂…则点B₄的坐标为（$\frac{8}{3}$，-$\frac{8}{3}$）．

Answer 1

分析 根据y=-x图象上的性质，分别得出A₂，A₃，A₄，B₁，B₂，B₃，B₄的坐标，进而得出答案．

解答 解：∵点A₁（0，-$\frac{1}{3}$）作y轴的垂线，交直线y=-x于点B₁，
则A₁B₁=$\frac{1}{3}$，
∴由题意可得：B₁（$\frac{1}{3}$，-$\frac{1}{3}$），
则A₂（0，-$\frac{2}{3}$），同理可得：B₂（$\frac{2}{3}$，-$\frac{2}{3}$），
则A₃（0，-$\frac{4}{3}$）同理可得：B₃（$\frac{4}{3}$，-$\frac{4}{3}$），
则A₄（0，-$\frac{8}{3}$）同理可得：B₄（$\frac{8}{3}$，-$\frac{8}{3}$）．
故答案为：（$\frac{8}{3}$，-$\frac{8}{3}$）．

点评 此题主要考查了点的坐标以及一次函数图象的性质，正确得出各点坐标是解题关键．