题目内容
如图,梯形ABCD中,AD∥BC,CE⊥AB于E,BF⊥CD于F,连接AF、DE.
(1)如图1,若AB=CD,且E、F两点分别在BA和CD的延长线上,在图中找出一个与∠BFA相等的角,如:∠BFA=
(2)如图2,若AB≠CD,且E在BA的延长线上,F在CD上,则(1)的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
(3)如图3,若AD⊥DE,AE=3AD,则tan∠BFA= .
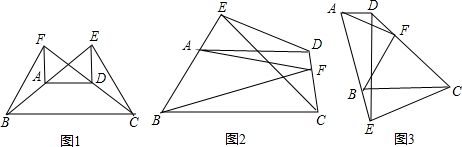
(1)如图1,若AB=CD,且E、F两点分别在BA和CD的延长线上,在图中找出一个与∠BFA相等的角,如:∠BFA=
(2)如图2,若AB≠CD,且E在BA的延长线上,F在CD上,则(1)的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
(3)如图3,若AD⊥DE,AE=3AD,则tan∠BFA=

考点:相似形综合题
专题:几何综合题
分析:(1)根据等腰梯形的性质,可得∠ABC与∠DCB的关系,根据AAS,可得△BEC与△CFB的关系,根据全等三角形的性质,可得BF与CE,根据SAS,可得△BAF与△CDE的关系,根据全等三角形的性质,可得答案;
(2)根据相似三角形的判定与性质,可得
=
,
=
,再根据相似三角形的判定,可得△OAF与△ODE△,根据相似三角形的性质,可得∠OED=∠OFA,根据余角的性质,可得答案;
(3)根据余角的性质,可得∠DAE与∠CED的关系,根据等量代换,可得∠BFA与∠EAD的关系,根据等角的正切相等,可得答案.
(2)根据相似三角形的判定与性质,可得
| OF |
| OE |
| OB |
| OC |
| OA |
| OD |
| OB |
| OC |
(3)根据余角的性质,可得∠DAE与∠CED的关系,根据等量代换,可得∠BFA与∠EAD的关系,根据等角的正切相等,可得答案.
解答:解:(1)AD∥BC,AB=CD,
∴∠ABC=∠DCB,
∵CE⊥AB于E,BF⊥CD于F,
∴∠BEC=∠CFB=90°,
在△BEC和△CFB中,
,
∴△BEC≌△CFB(AAS),
∴CE=BF,∠BCE=∠CBF,
∵∠ABC=∠DCB,
∴∠ABF=∠DCE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
∴∠BFA=∠CED,
故答案为:∠CED;
(2)如图一:延长BA、CD交于O, ,
,
(1)中的结论仍然成立,
证明:∵CE⊥AB于E,BF⊥CD于F,
∴∠CEO=∠∠FO=90°,∠O=∠O,
∴△CEO∽△BFO,
∴
=
.
∵AD∥BC,
∴△ADO∽△BCO,
∴
=
,
=
,
∴
=
,∠O=∠O,
∴△OED∽△OFA,
∴∠OED=∠OFA,
∠CED+∠OED=90°,∠BFA+∠OFA=90°,
∴∠CED=∠BFA;
(3)如图二: ,
,
CE⊥AB于E,BF⊥CD于F,
由(2)中的结论得∠CED=∠BFA,
∵AD⊥DE,
∴∠ADE=∠CEB=90°,
由勾股定理得DE=2
AD,
∠EAD+∠AED=90°,∠AED+∠DEC=90°,
∴∠EAD=∠CED=∠BFA.
∴tan∠BFA=tan∠EAD=
=
=2
,
故答案为:2
.
∴∠ABC=∠DCB,
∵CE⊥AB于E,BF⊥CD于F,
∴∠BEC=∠CFB=90°,
在△BEC和△CFB中,
|
∴△BEC≌△CFB(AAS),
∴CE=BF,∠BCE=∠CBF,
∵∠ABC=∠DCB,
∴∠ABF=∠DCE,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(SAS),
∴∠BFA=∠CED,
故答案为:∠CED;
(2)如图一:延长BA、CD交于O,
 ,
,(1)中的结论仍然成立,
证明:∵CE⊥AB于E,BF⊥CD于F,
∴∠CEO=∠∠FO=90°,∠O=∠O,
∴△CEO∽△BFO,
∴
| OE |
| OF |
| OC |
| OB |
∵AD∥BC,
∴△ADO∽△BCO,
∴
| OA |
| OB |
| OD |
| OC |
| OC |
| OB |
| OD |
| OA |
∴
| OE |
| OF |
| OD |
| OA |
∴△OED∽△OFA,
∴∠OED=∠OFA,
∠CED+∠OED=90°,∠BFA+∠OFA=90°,
∴∠CED=∠BFA;
(3)如图二:
 ,
,CE⊥AB于E,BF⊥CD于F,
由(2)中的结论得∠CED=∠BFA,
∵AD⊥DE,
∴∠ADE=∠CEB=90°,
由勾股定理得DE=2
| 2 |
∠EAD+∠AED=90°,∠AED+∠DEC=90°,
∴∠EAD=∠CED=∠BFA.
∴tan∠BFA=tan∠EAD=
| DE |
| AD |
2
| ||
| AD |
| 2 |
故答案为:2
| 2 |
点评:本题考查了相似形综合题,利用了全等三角形的判定与性质,相似三角形的判定与性质,余角的性质,题目有点难度,(2)中构造出相似三角形是解题关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
如图各曲线中,不表示y是x的函数的是( )
A、 |
B、 |
C、 |
D、 |
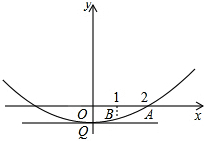 如图,在平面直角坐标系中,已知二次函数
如图,在平面直角坐标系中,已知二次函数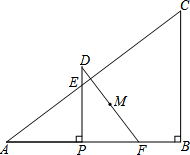 如图,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,动点P从点A出发,以每秒4cm的速度沿AB方向运动,到达点B时停止运动.过点P作AB的垂线交斜边AC于点E,将△APE绕点P顺时针旋转90°得到△DPF.设点P在边AB上运动的时间为t(秒).
如图,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,动点P从点A出发,以每秒4cm的速度沿AB方向运动,到达点B时停止运动.过点P作AB的垂线交斜边AC于点E,将△APE绕点P顺时针旋转90°得到△DPF.设点P在边AB上运动的时间为t(秒).