题目内容
因式分解下列各式：
（1）4a2x2-12a3x4-ax；
（2）am+am-1+am-2（m为正整数，且m≥3）；
（3）10（a-b）2-5（b-a）3；
（4）-8（m-n）3+4n（n-m）3．
（1）4a2x2-12a3x4-ax；
（2）am+am-1+am-2（m为正整数，且m≥3）；
（3）10（a-b）2-5（b-a）3；
（4）-8（m-n）3+4n（n-m）3．
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式提取公因式即可得到结果；
（2）原式提取公因式即可得到结果；
（3）原式提取公因式即可得到结果；
（4）原式变形后，提取公因式即可得到结果．
（2）原式提取公因式即可得到结果；
（3）原式提取公因式即可得到结果；
（4）原式变形后，提取公因式即可得到结果．
解答：解：（1）原式=ax（4ax-12a2x3-1）；
（2）原式=am-2（a2+a+1）；
（3）原式=5（a-b）2（2+a-b）；
（4）原式=8（n-m）3+4n（n-m）3=4（n-m）3（2+n）．
（2）原式=am-2（a2+a+1）；
（3）原式=5（a-b）2（2+a-b）；
（4）原式=8（n-m）3+4n（n-m）3=4（n-m）3（2+n）．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
计算x5•x5的值为（ ）
| A、x5 |
| B、x10 |
| C、x25 |
| D、2x5 |
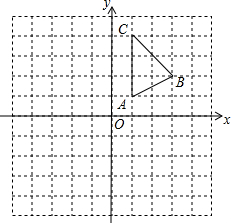在平面直角坐标系中，△ABC的三个顶点坐标分别为：A（1，1），B（3，2），C（1，4）．
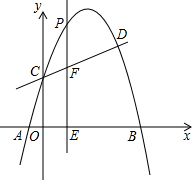已知抛物线y=-x2+