题目内容
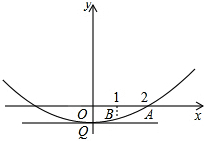 如图,在平面直角坐标系中,已知二次函数y=
如图,在平面直角坐标系中,已知二次函数y=| 1 |
| 4 |
| 3 |
| 4 |
(1)求该二次函数的表达式;
(2)设抛物线上有一动点P从点B处出发沿抛物线向上运动,其纵坐标y1随时间t(t≥0)的变化规律为y1=-
| 3 |
| 4 |
①当点P在起始位置点B处时,试判断直线l与圆C的位置关系,并说明理由;在点P运动的过程中,直线l与圆C是否始终保持这种位置关系?请说明你的理由;
②若在点P开始运动的同时,直线l也向上平行移动,且垂足Q的纵坐标y2随时间t的变化规律y2=-1+3t,则当t在什么范围内变化时,直线l与圆C相交?
考点:二次函数综合题
专题:
分析:(1)所求函数的解析式中有两个待定系数,直接将A、B两点坐标代入即可得解.
(2)①由于OP是⊙C的直径,根据P点的纵坐标可表示出C点的纵坐标,进而能表示出C到直线l的距离;OP长易得,然后通过比较⊙C的半径和C到直线l的距离,即可判定直线l与⊙C的位置关系.
②该题要分两问来答,首先看第一问;该小题的思路和①完全一致,唯一不同的地方:要注意直线l与点C的位置关系(需要考虑到C到直线l的表达方式).
(2)①由于OP是⊙C的直径,根据P点的纵坐标可表示出C点的纵坐标,进而能表示出C到直线l的距离;OP长易得,然后通过比较⊙C的半径和C到直线l的距离,即可判定直线l与⊙C的位置关系.
②该题要分两问来答,首先看第一问;该小题的思路和①完全一致,唯一不同的地方:要注意直线l与点C的位置关系(需要考虑到C到直线l的表达方式).
解答:解:(1)将点A(2,0)和点B(1,-
)分别代入y=
x2+mx+n中,得:
,
解得:
.
∴抛物线的解析式:y=
x2-1;
(2)①将P点纵坐标代入(1)的解析式,得:
x2-1=-
+2t,x=
,
∴P(
,-2t),
∴圆心C(
,-
+t),
∴点C到直线l的距离:-
+t-(-1)=t+
;
而OP2=8t+1+(-
+2t)2,得OP=2t+
,半径OC=t+
;
∴直线l与⊙C始终保持相切;
②当圆心C在直线l上时,-
+t=-1+3t,t=
;
此时直线l与⊙C相交;
当0<t≤
时,C到直线l的距离:-
+t-(-1+3t)=
-2t<t+
,
∴直线l与⊙C相交;
当t>
时,C到直线l的距离:-1+3t-(-
+t)=2t-
,
若直线l与⊙C相交,则:2t-
<t+
,t<
;
综上,当0<t<
时,直线l与⊙C相交.
| 3 |
| 4 |
| 1 |
| 4 |
|
解得:
|
∴抛物线的解析式:y=
| 1 |
| 4 |
(2)①将P点纵坐标代入(1)的解析式,得:
| 1 |
| 4 |
| 3 |
| 4 |
| 8t+1 |
∴P(
| 8t+1 |
∴圆心C(
| ||
| 2 |
| 3 |
| 4 |
∴点C到直线l的距离:-
| 3 |
| 8 |
| 5 |
| 8 |
而OP2=8t+1+(-
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
| 8 |
∴直线l与⊙C始终保持相切;
②当圆心C在直线l上时,-
| 3 |
| 8 |
| 5 |
| 16 |
此时直线l与⊙C相交;
当0<t≤
| 5 |
| 16 |
| 3 |
| 8 |
| 5 |
| 8 |
| 5 |
| 8 |
∴直线l与⊙C相交;
当t>
| 5 |
| 16 |
| 3 |
| 8 |
| 5 |
| 8 |
若直线l与⊙C相交,则:2t-
| 5 |
| 8 |
| 5 |
| 8 |
| 5 |
| 4 |
综上,当0<t<
| 5 |
| 4 |
点评:本题考查的是二次函数的综合题型,该题是函数的动点问题,其中涉及直线与圆的位置关系等综合知识;在处理此类问题时,要注意寻找关键点以及分段进行讨论,以免出现漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
实数
的值等于( )
| 16 |
| A、±4 | B、±2 | C、4 | D、2 |
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的不等式k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图,则关于x的不等式k2x>k1x+b的解集为( )| A、x<-1 | B、x>1 |
| C、x<3 | D、x>3 |
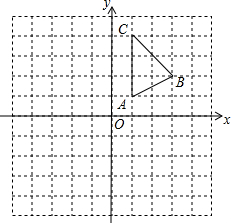 在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4). 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,