题目内容
6.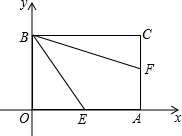 如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.
如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.(1)求证:四边形OACB是矩形;
(2)若点E是边OA的中点,且∠OBE=∠EBF,试探究线段AF、AC、BF之间的数量关系,并说明理由;
(3)在(2)条件下,若BE=8,BF=10,求点F的坐标.
分析 (1)根据一组对边平行且相等的四边形是平行四边形,得出四边形OACB是平行四边形,再根据∠BOA=90°,得出四边形OACB是矩形;
(2)过点E作DE⊥BF,垂足为D,根据AAS证出Rt△BOE≌Rt△BDE,得出OB=BD,OE=DE,∠BED=∠BEO=$\frac{1}{2}$∠OED,再根据点E是边OA的中点,AE=DE,
在Rt△DEF和Rt△AEF中,根据HL得出Rt△DEF≌Rt△AEF,得出AF=DF,再根据矩形的性质得出线段AF、AC、BF之间的数量关系;
(3)根据∠BED=∠BEO,∠DEF=∠FEA,得出∠BEF=90°,在Rt△BEF中,设DF=x,BD=10-x,根据BE2-BD2=EF2-DF2,再根据求出x的值,再根据DE2=EF2-DF2,求出DE,从而得出点F的坐标.
解答  解:(1)证明:∵OB∥AC,OB=AC,
解:(1)证明:∵OB∥AC,OB=AC,
∴四边形OACB是平行四边形,
∵∠BOA=90°,
∴四边形OACB是矩形;
(2)过点E作DE⊥BF,垂足为D,连接EF,
∴∠BOE=∠BDE=90°,
在Rt△BOE和Rt△BDE中,
∵$\left\{\begin{array}{l}{∠BOE=∠BDE=90°}\\{∠OBE=∠EBF}\\{BE=BE}\end{array}\right.$,
∴Rt△BOE≌Rt△BDE,
∴OB=BD,OE=DE,∠BED=∠BEO=$\frac{1}{2}$∠OED,
∵点E是边OA的中点,
∴AE=OE,
∴AE=DE,
在Rt△DEF和Rt△AEF中,
$\left\{\begin{array}{l}{AE=AD}\\{EF=EF}\end{array}\right.$,
∴Rt△DEF≌Rt△AEF,
∴AF=DF,
∵四边形OACB是矩形,
∴AC=OB,
∴BF=BD+DF=OB+AF=AC+AF;
(3)∵Rt△DEF≌Rt△AEF,
∴∠DEF=∠FEA=$\frac{1}{2}$∠DEA,
∴∠BEF=∠DEF+∠BED=$\frac{1}{2}$∠DEA+$\frac{1}{2}$∠OED=$\frac{1}{2}$(∠DEA+∠OED)=90°,
在Rt△BEF中,设DF=x,BD=10-x,
∵BE2-BD2=EF2-DF2,
∴82-(10-x)2=62-x2,
∴x=3.6,
∵DE2=EF2-DF2,
∴DE2=62-3.62,
∴DE=4.8,OA=2DE=9.6,
∴点F的坐标为(9.6,4.8).
点评 此题考查了四边形,用到的知识点是平行四边形的判定、矩形的判定与性质、全等三角形的判定、勾股定理,关键是根据题意作出辅助线,构造直角三角形.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 6,7,8 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
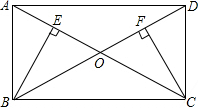 如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:
如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证: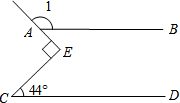 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.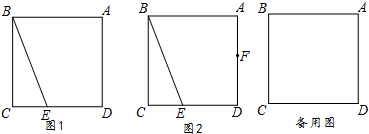
 下图中有两个变量,你能将其中一个变量看做另一个变量的函数吗?
下图中有两个变量,你能将其中一个变量看做另一个变量的函数吗?