题目内容
18.在正方形ABCD中,E为边CD上一点,连接BE.(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;
(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;
(3)在(2)的条件下,若点E为边CD的三等分点,且CE<DE,请写出求cos∠FED的思路.(可以不写出计算结果).
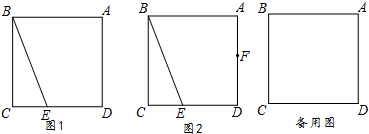
分析 (1)由题意画出图形即可;
(2)根据正方形的性质,判断出△BAF≌△BCG,再判断出△BEF≌△BEG即可;
(3)由题意表示出线段,再用EF2=DF2+DE2,列出方程,解出即可.
解答 (1)补全图形,如图1所示,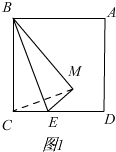
∠ABF与∠CBE的数量关系为:∠ABF+CBE=45°,
证明:如图2,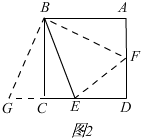
连接BF,EF,延长DC到G,使CG=AF,连接BG,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCD=∠ABC=90°,
∴△BAF≌△BCG,
∴BF=BG,∠ABF=∠CBG,
∵AF+CE=EF,
∴EF=GE,
∴△BEF≌△BEG,
∴∠FBE=∠GBE=∠ABF+∠CBE,
∴∠ABF+∠CBE=45°.
(3)解:设正方形的边长为3a,AF=x,
∵点E是CD三等分点
∴EF=CG+CE=x+a,DE=2a,DF=3a-x,
在Rt△DEF中,EF2=DF2+DE2,
∴(x+a)2=(3a-x)2+(2a)2,
∴x=$\frac{3}{2}$a,
∴EF=x+a=$\frac{3}{2}$a+a=$\frac{5}{2}$,
∴cos∠FED=$\frac{DE}{EF}$=$\frac{2a}{\frac{5}{2}a}$=$\frac{4}{5}$.
点评 此题是四边形综合题,主要考查了正方形的性质,三角形的全等,勾股定理,三角函数,判断三角形全等(△BEF≌△BEG)解本题的关键,点E是CD三等分点的运用是解本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
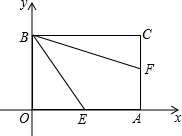 如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.
如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC. 如图,点M、N分别在直线a、b上,且a∥b,P为两平行线间一点,那么∠1+∠2+∠3=360°.
如图,点M、N分别在直线a、b上,且a∥b,P为两平行线间一点,那么∠1+∠2+∠3=360°.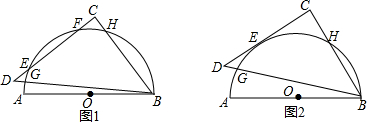
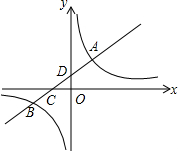 如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.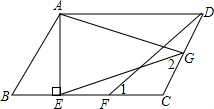 已知,如图,在?ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知,如图,在?ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF,EG,AG,∠1=∠2.