题目内容
16.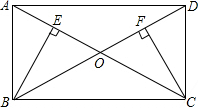 如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:
如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:(1)BE=CF;
(2)△CDF∽△BDC.
分析 (1)根据矩形的性质得出AC=BD,AO=OC,BO=DO,推出OB=OC,求出∠ECB=∠FBC,∠BEC=∠CFB=90°,根据AAS推出△BEC≌△CFB,即可得出答案;
(2)根据矩形的性质求出∠BCD=90°,求出∠CFD=∠BCD,根据相似三角形的性质得出即可.
解答 证明:(1)∵四边形ABCD是矩形,
∴AC=BD,AO=OC,BO=DO,
∴OB=OC,
∴∠ECB=∠FBC,
∵BE⊥AC,CF⊥BD,
∴∠BEC=∠CFB=90°,
在△BEC和△CFB中
$\left\{\begin{array}{l}{∠ECB=∠FBC}\\{∠BEC=∠CFB}\\{BC=CB}\end{array}\right.$
∴△BEC≌△CFB(AAS),
∴BE=CF;
(2)∵四边形ABCD是矩形,
∴∠BCD=90°,
∵CF⊥BD,
∴∠CFD=90°,
∴∠CFD=∠BCD,
∵∠FDC=∠CDB,
∴△CDF∽△BDC.
点评 本题考查矩形的性质,全等三角形的性质和判定,相似三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.

练习册系列答案
相关题目
5.下列真命题中,它的逆命题也是真命题的是( )
| A. | 全等三角形的对应角相等 | |
| B. | 对顶角相等 | |
| C. | 等边三角形是锐角三角形 | |
| D. | 直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半 |
 如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.
如图,Rt△ABO中,∠AOB=90°,∠ABO=30°,点A在第二象限,点B在第一象限,过点A的反比例函数表达式为y=-$\frac{1}{x}$,则过点B的反比例函数表达式为y=$\frac{3}{x}$.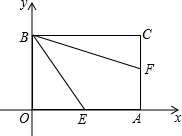 如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.
如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.