题目内容
9.如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图2围成一个较大的正方形.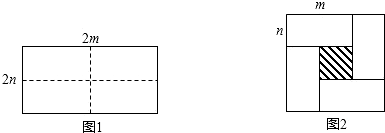
(1)图2中的阴影部分的正方形的边长可表示为m-n;
(2)请用两种不同的方法表示图2中阴影部分的面积:
方法1:(m-n)2;
方法2:(m+n)2-4mn;
(3)观察图2,请你写出下列三个代数式之间的等量关系:
代数式:(m+n)2,(m-n)2,mn.(m-n)2=(m+n)2-4mn;
(4)根据(3)题中的等量关系,解决问题:
若m+n=5,mn=4,求m-n的值.
分析 (1)阴影部分的正方形的边长=小矩形的长-小矩形的宽;
(2)阴影部分的面积可以看作是边长(m-n)的正方形的面积,也可以看作边长(m+n)的正方形的面积减去4个小长方形的面积;
(3)由(2)的结论根据面积相等直接写出即可;
(4)利用(3)的结论:(m-n)2=(m+n)2-4mn,把数值整体代入即可.
解答 解:(1)阴影部分的正方形的边长可表示为:m-n;
(2)阴影部分的面积为:(m-n)2,也可表达为:(m+n)2-4mn;
(3)等量关系式:(m-n)2=(m+n)2-4mn;
(4)当m+n=5,mn=4时,
(m-n)2=(m+n)2-4mn
=52-4×4
=9,
则m-n=±3.
点评 本题考查了完全平方公式,对几何图形的整体分析,对完全平方公式的灵活应用变形整理是解此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.圆锥体是由下列哪个图形绕自身的对称轴旋转一周得到的( )
| A. | 正方形 | B. | 等腰三角形 | C. | 圆 | D. | 等腰梯形 |
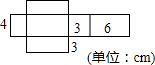 如图是一个长方体纸盒的展开图,这个纸盒的表面积是108cm2,体积是72cm3.
如图是一个长方体纸盒的展开图,这个纸盒的表面积是108cm2,体积是72cm3.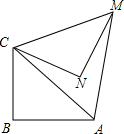 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.