题目内容
18.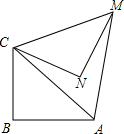 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.
分析 由勾股定理求出CA,由旋转的性质得出CA=CM,∠ACM=60°,证出△ACM为等边三角形,得出AM=CA即可.
解答 解:∵∠ABC=90°,AB=BC=$\sqrt{2}$,
∴CA=$\sqrt{A{B}^{2}+B{C}^{2}}$=2,
由旋转的性质得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CA=2;
故答案为:2.
点评 本题考查了图形的变换-旋转,等腰直角三角形的性质,等边三角形的判定和性,勾股定理;熟练掌握旋转的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.有50个同学排成一队,第一次从前往后报数(按1,2,3,…的顺序),报到奇数的同学退出队伍,第二次从后往前报数(按1,2,3,…的顺序),报到奇数的同学退出队伍,第三次又从前往后报数,第四次又从后往前报数,如此继续下去…则最后留下来的同学第一次报的数是( )
| A. | 16 | B. | 24 | C. | 32 | D. | 48 |
13.若(x+2)(x-a)=x2+bx-10,则b的值为( )
| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
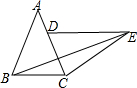 △ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.
△ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.
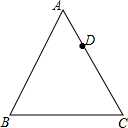 如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$.
如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$.