题目内容
1.计算:(1)(-a2b)2•2ab;
(2)(x+3)(x-4);
(3)(2a-3b)2+(2a+3b)(2a-3b);
(4)2012+1992.(运用乘法公式计算)
分析 (1)根据整式的混合运算的运算顺序,首先计算乘方,然后计算乘法,求出算式的值是多少即可.
(2)根据多项式乘以多项式的运算方法,求出算式的值是多少即可.
(3)根据整式的混合运算的运算顺序,首先计算乘方,然后计算乘法,最后计算加法,求出算式的值是多少即可.
(4)首先把2012+1992化为(200+1)2+(200-1)2,然后运用完全平方公式,求出算式的值是多少即可.
解答 解:(1)(-a2b)2•2ab
=a4b2•2ab
=2a5b3
(2)(x+3)(x-4)
=x•x-4x+3x-3×4
=x2-x-12
(3)(2a-3b)2+(2a+3b)(2a-3b)
=4a2-12ab+9b2+4a2-9b2
=8a2-12ab
(4)2012+1992
=(200+1)2+(200-1)2
=2002+400+1+2002-400+1
=40000+400+1+40000-400+1
=80002
点评 此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.小明在做数学题时,发现下面有趣的结果:
3-2=1
8+7-6-5=4
15+14+13-12-11-10=9
24+23+22+21-20-19-18-17=16
…
根据以上规律可知第10行左起第一个数是( )
3-2=1
8+7-6-5=4
15+14+13-12-11-10=9
24+23+22+21-20-19-18-17=16
…
根据以上规律可知第10行左起第一个数是( )
| A. | 100 | B. | 121 | C. | 120 | D. | 82 |
12. 如图,在?ABCD中,∠A=65°,将?ABCD绕顶点B顺时针旋转到?A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1的大小为( )
如图,在?ABCD中,∠A=65°,将?ABCD绕顶点B顺时针旋转到?A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1的大小为( )
 如图,在?ABCD中,∠A=65°,将?ABCD绕顶点B顺时针旋转到?A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1的大小为( )
如图,在?ABCD中,∠A=65°,将?ABCD绕顶点B顺时针旋转到?A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1的大小为( )| A. | 45° | B. | 50° | C. | 65° | D. | 70° |
13.若(x+2)(x-a)=x2+bx-10,则b的值为( )
| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
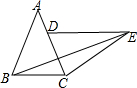 △ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.
△ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.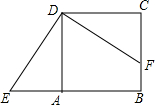 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.