题目内容
19.将一副直角三角板如图①摆放,等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,如图②,若BF=12,求DF的长.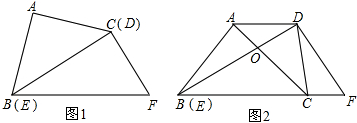
分析 由三角板的特点直接得到∠DEF=30°,再用锐角三角函数求解.
解答 解:在Rt△DEF中,∠DEF=30°,BF=12,
∴sin∠DEF=$\frac{DF}{BF}$,
∴DF=BF×sin∠DEF=12×$\frac{1}{2}$=6.
点评 此题是旋转的性质题,主要考查了锐角三角函数的意义,解本题的关键是掌握锐角三角函数的意义.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
9.(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
| 球的类别 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
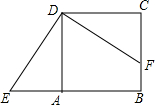 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.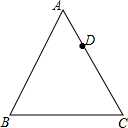 如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$.
如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$.