题目内容
1. 如图,在△ABC中,∠A=65°,∠1=22°,∠2=35°,求∠BDC.
如图,在△ABC中,∠A=65°,∠1=22°,∠2=35°,求∠BDC.
分析 先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由∠1=22°,∠2=35°求出∠DBC+∠DCB的度数,由三角形内角和定理即可得出结
解答 解:∵在△ABC中,∠A=65°,
∴∠ABC+∠ACB=180°-65°=115°.
∵∠1=22°,∠2=35°,
∴∠DBC+∠DCB=∠ABC+∠ACB-∠1-∠2=115°-22°-35°=65°.
∴∠BDC=180°-(∠DBC+∠DCB)=180°-65°=115°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
4.已知x2+4-4x+y2+2xy-4y=0,则x+y=( )
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |
2.一套运动服原价a元,连续两次降价x%后售价为b元,下面所列方程中正确的是( )
| A. | b(1+x%)2=a | B. | a(1-x%)2=b | C. | a(1+x%)2=b | D. | a(1-2x%)=b |
 如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的结论有①②(填上序号即可)
如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的结论有①②(填上序号即可)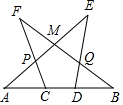 如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对.
如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对. 如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F=360°. 如图,⊙O的直径为5,△ABC为⊙O的内接三角形,CD⊥AB于D,AC=2$\sqrt{6}$,求sin∠BCD的值.
如图,⊙O的直径为5,△ABC为⊙O的内接三角形,CD⊥AB于D,AC=2$\sqrt{6}$,求sin∠BCD的值. 如图,函数y=-2x与y=$\frac{k}{x}$的图象相交于A(m,2)、B两点.
如图,函数y=-2x与y=$\frac{k}{x}$的图象相交于A(m,2)、B两点. 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.