题目内容
2．已知p为偶数，q为奇数，方程组$\left\{\begin{array}{l}{x-2012y=p}\\{2013x+3y=q}\end{array}\right.$的解是整数，那么（ ）| A． | x为奇数，y是偶数 | B． | x为偶数，y是奇数 | C． | x为偶数，y是偶数 | D． | x为奇数，y是奇数 |
分析 根据第一个方程及p为偶数可知x为偶数，根据第二个方程及q为偶数可知y为奇数．
解答 解：由方程组$\left\{\begin{array}{l}{x-2102y=p①}\\{2013x+3y=q②}\end{array}\right.$，
以及p为偶数，q为奇数，其解x，y又是整数．
由①可知x为偶数，由②可知y是奇数，
故选B．
点评 此题考查的是解二元一次方程组和奇偶数的性质，准确掌握奇偶数的运算性质是解题的关键．
练习册系列答案
相关题目
如图所示，在四边形ABCD中，AB⊥BC，AC⊥CD，以CD为直径作半圆O，AB=4cm，BC=3cm，AD=13cm．求图中阴影部分的面积：
10．
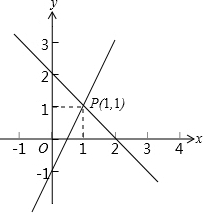用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象如图所示，则所解的二元一次方程组是（ ）
用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象如图所示，则所解的二元一次方程组是（ ）| A． | $\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{2x-y=1}\\{3x-2y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{2x-y=1}\\{3x+2y=5}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=2}\\{3x-2y=1}\end{array}\right.$ |
如图，把一张长方形纸片ABCD沿EF折叠，C点落在C′处，D点落在D′处，ED′交BC于点G．已知∠EFG=50°．则∠BGD′的度数为80°．
如图，在?ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于F．