题目内容
14. 如图,在?ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
如图,在?ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求?ABCD的面积.
分析 (1)由平行四边形的性质和已知条件得出∠AEB=∠CBF,∠ABE=∠F=20°,证出∠AEB=∠ABE=20°,由三角形内角和定理求出结果即可;
(2)求出DE,由勾股定理求出CE,即可得出结果.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,CD=AB=5,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=20°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=20°,
∴AE=AB,∠A=(180°-20°-20°)÷2=140°;
(2)∵AE=AB=5,AD=BC=8,CD=AB=5,
∴DE=AD-AE=3,
∵CE⊥AD,
∴CE=$\sqrt{C{D}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴?ABCD的面积=AD•CE=8×4=32.
点评 本题主要考查了平行四边形的性质,等腰三角形的判定、勾股定理;熟练掌握平行四边形的性质,证出∠AEB=∠ABE是解决问题的关键.

练习册系列答案
相关题目
2.已知p为偶数,q为奇数,方程组$\left\{\begin{array}{l}{x-2012y=p}\\{2013x+3y=q}\end{array}\right.$的解是整数,那么( )
| A. | x为奇数,y是偶数 | B. | x为偶数,y是奇数 | C. | x为偶数,y是偶数 | D. | x为奇数,y是奇数 |
19.下列各式运算正确的是( )
| A. | a-(-a)=0 | B. | a+(-a)=0 | C. | a•(-a)=a2 | D. | a÷(-$\frac{1}{a}$)=-1 |
3.若$\sqrt{x+3}$=3,则(x+3)2的平方根是( )
| A. | 81 | B. | ±81 | C. | ±9 | D. | ±3 |
4.下列各式属于最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{6}$ | D. | $\sqrt{8}$ |
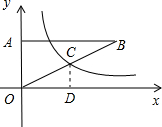 如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.
如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.