题目内容
10.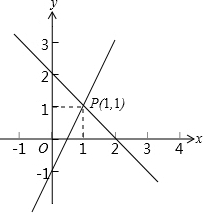 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )
用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )| A. | $\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=1}\\{3x-2y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x-y=1}\\{3x+2y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=2}\\{3x-2y=1}\end{array}\right.$ |
分析 由于函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应先用待定系数法求出两条直线的解析式,联立两个函数解析式所组成的方程组即为所求的方程组.
解答 解:根据给出的图象上的点的坐标,(0,-1)、(1,1)、(0,2);
分别求出图中两条直线的解析式为y=2x-1,y=-x+2,
因此所解的二元一次方程组是$\left\{\begin{array}{l}{x+y=2}\\{2x-y=1}\end{array}\right.$.
故选A.
点评 本题考查了一次函数与二元一次方程组,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | $\sqrt{28}$×$\frac{1}{2}$=$\sqrt{14}$ | B. | $\sqrt{(a-b)^{2}}$•$\frac{1}{a-b}$=1 | ||
| C. | -2x2-3x+5=(1-x)(2x+5) | D. | (-a)7÷a3=a4 |
2.已知p为偶数,q为奇数,方程组$\left\{\begin{array}{l}{x-2012y=p}\\{2013x+3y=q}\end{array}\right.$的解是整数,那么( )
| A. | x为奇数,y是偶数 | B. | x为偶数,y是奇数 | C. | x为偶数,y是偶数 | D. | x为奇数,y是奇数 |
19.下列各式运算正确的是( )
| A. | a-(-a)=0 | B. | a+(-a)=0 | C. | a•(-a)=a2 | D. | a÷(-$\frac{1}{a}$)=-1 |
20.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
 如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM,请判断AM与⊙O的位置关系,并说明理由.
如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM,请判断AM与⊙O的位置关系,并说明理由.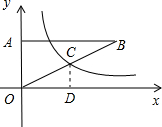 如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.
如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.