Question

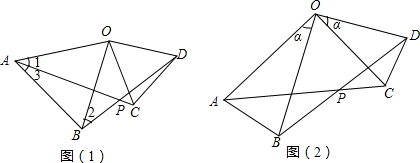
已知：如图（1），△AOB和△COD都是等边三角形，连接AC、BD交于点P．
（1）求证：AC=BD；
（2）求∠APB的度数；
（3）如图（2），将（1）中的△AOB和△COD改为等腰三角形，并且OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD的等量关系为

 

，∠APB的大小为

 

．

Answer 1

考点：全等三角形的判定与性质,等边三角形的性质

专题：

分析：（1）根据等边三角形性质得出AO=OB，CO=DO，∠AOB=∠COD=60°，求出∠AOC=∠BOD，证出△AOC≌△BOD即可；
（1）根据全等得出∠1=∠2，根据三角形内角和定理求出即可；
（3）求出∠AOC=∠BOD，证出△AOC≌△BOD，推出AC=BD，∠OCA=∠ODB，根据三角形内角和定理求出即可

解答：（1）证明：∵△AOB和△COD都是等边三角形，
∴AO=OB，CO=DO，∠AOB=∠COD=60°，
∴∠AOC=∠BOD=60°+∠BOC，
在△AOC和△BOD中，

AO=OB ∠AOC=∠BOD OC=OD

，
∴△AOC≌△BOD（SAS），
∴AC=BD；

（2）解：∵△ABO是等边三角形，
∴∠OAB=∠OBA=60°，
∴∠1+∠3=60°，
∵△AOC≌△BOD，
∴∠1=∠2，
∴∠APB=180°-（∠3+∠ABO+∠2）
=180°-（∠3+∠1+∠ABO）
=180°-（60°+60°）
=60°；

（3）解：AC=BD，∠APB=α，
理由是：∵∠AOB=∠COD=α，
∴∠AOC=∠BOD=∠BOC+α，
在△AOC和△BOD中

AO=OB ∠AOC=∠BOD OC=OD

∴△AOC≌△BOD（SAS），
∴AC=BD，∠OCA=∠ODB，
∴∠APB=180°-（∠PDC+∠PCO+∠OCD）
=180°-（∠PDC+∠BDO+∠OCD）
=180°-（∠ODC+∠OCD）
=∠DOC
=α，
故答案为：AC=BD，∠APB=α．

点评：本题考查了等边三角形的性质，全等三角形的性质和判定的应用，主要考查学生的推理能力，题目比较典型，证明过程类似．