题目内容
14. 如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
分析 点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,利用tanA=$\frac{1}{3}$得到tan∠BCB′=$\frac{BB′}{B′C}$=$\frac{1}{3}$,然后设B′B=x,则B′C=3x,在Rt△B′CB中,利用勾股定理求得答案即可.
解答  解:如图,点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,
解:如图,点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,
∵tanA=$\frac{1}{3}$,
∴tan∠BCB′=$\frac{BB′}{B′C}$=$\frac{1}{3}$,
∴设B′B=x,则B′C=3x,
在Rt△B′CB中,
B′B2+B′C2=BC2,
即:x2+(3x)2=($\sqrt{5}$)2,
x=$\frac{\sqrt{2}}{2}$(负值舍去),
∴BD=B′C=$\frac{3\sqrt{2}}{2}$,
点评 本题考查了解直角三角形的应用,解题的关键是能够从实际问题中整理出直角三角形,难度不大.

练习册系列答案
相关题目
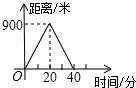
4. 如图,函数y=2x和y=ax+3(a≠0)的图象相交于点A(m,2),则不等式0<ax+3<2x的解集为( )
如图,函数y=2x和y=ax+3(a≠0)的图象相交于点A(m,2),则不等式0<ax+3<2x的解集为( )
 如图,函数y=2x和y=ax+3(a≠0)的图象相交于点A(m,2),则不等式0<ax+3<2x的解集为( )
如图,函数y=2x和y=ax+3(a≠0)的图象相交于点A(m,2),则不等式0<ax+3<2x的解集为( )| A. | x<1 | B. | x>1 | C. | 0<x<1 | D. | 1<x<3 |
5.函数y=$\sqrt{5-x}$自变量x的取值范围是( )
| A. | x>5 | B. | x≥5 | C. | x<5 | D. | x≤5 |


 如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH. 如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )
如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )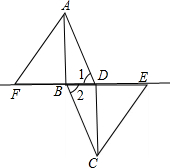 如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )