题目内容
4．
如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是$\widehat{ABC}$上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
分析 根据四边形的内角和，可得∠BOA，根据等弧所对的圆周角相等，根据圆周角定理，可得答案．
解答 解；如图
，
由四边形的内角和定理，得
∠BOA=360°-90°-90°-80°=100°，
由$\widehat{AC}$=$\widehat{BC}$，得
∠AOC=∠BOC=50°．
由圆周角定理，得
∠ADC=$\frac{1}{2}$∠AOC=25°，
故选：C．
点评 本题考查了切线的性质，切线的性质得出$\widehat{AC}$=$\widehat{BC}$是解题关键，又利用了圆周角定理．
练习册系列答案
相关题目
如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图．已知长方体货厢的高度BC为$\sqrt{5}$米，tanA=$\frac{1}{3}$，现把图中的货物继续往前平移，当货物顶点D与C重合时，仍可把货物放平装进货厢，求BD的长．（结果保留根号）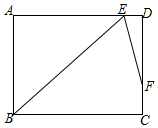
如图，在矩形ABCD中，∠B的平分线BE与AD交于点E，∠BED的平分线EF与DC交于点F，若AB=9，DF=2FC，则BC=$6\sqrt{2}+3$．（结果保留根号）
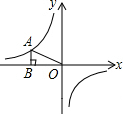如图，点A为反比例函数$y=-\frac{4}{x}$图象上一点，过A作AB⊥x轴于点B，连接OA，则△ABO的面积为（ ）
16．下列图形中既是中心对称图形又是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
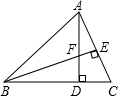如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．