题目内容
19. 如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )
如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 在Rt△ACB中,根据勾股定理求得BC边的长度,然后由三角形中位线定理知DE=$\frac{1}{2}$BC.
解答 解:∵在Rt△ACB中,∠ACB=90°,AC=8,AB=10,
∴BC=6.
又∵DE垂直平分AC交AB于点E,
∴DE∥BC,
∴DE是△ACB的中位线,
∴DE=$\frac{1}{2}$BC=3.
故选:D.
点评 本题考查了三角形中位线定理、勾股定理.三角形中位线的性质:三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
9.为了了解居民节约用水情况,小明同学对本单元的住户当月用水量进行了调查,情况如表:
则关于这12户居民月用水量,下列说法错误的是( )
| 住户(户) | 2 | 4 | 5 | 1 |
| 月用水量(方/户) | 2 | 4 | 6 | 10 |
| A. | 平均数是5 | B. | 众数是6 | C. | 极差是8 | D. | 中位数是6 |
4.下列计算中,正确的是( )
| A. | (a3)4=a12 | B. | a3•a5=a15 | C. | a2+a2=a4 | D. | a6÷a2=a3 |
11.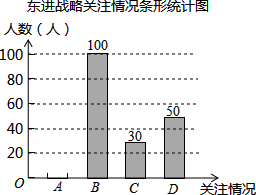 深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
(1)根据上述统计图可得此次采访的人数为200人,m=20,n=0.15;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有1500人.
 深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | M | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | N |
| D.不知道 | 50 | 0.25 |
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有1500人.
8.一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取2个球,则取到的是一个红球、一个白球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
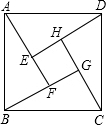 如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为$\frac{2}{3}$.
如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为$\frac{2}{3}$.
 如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为$\sqrt{5}$米,tanA=$\frac{1}{3}$,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)