题目内容
18．
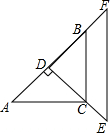已知：有两块完全相同的含45°角的三角板，如图，将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处，这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$．
分析 根据D为AB的中点，得出S△ABC=2S△DBC，即可得出．
解答 解：∵在直角△ABC中，D为斜边AB的中点，
∴AD=BD=CD=$\frac{1}{2}$AB，CD⊥AB，
∵S△ABC=$\frac{1}{2}$AB×CD，S△DBC=$\frac{1}{2}$BD×CD，
∴S△DBC=$\frac{1}{2}$S△ABC
故答案为$\frac{1}{2}$．
点评 本题考查了等腰直角三角形的性质，关键是根据D为AB的中点得出其面积关系．
练习册系列答案
相关题目
9．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，CD是AB边上的高，则AD长为（ ）cm．
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{16}{5}$ | D． | $\frac{9}{5}$ |
6．十一旅游黄金周期间，某景点举办优惠活动，成人票和儿童票均有较大折扣，王明家去了3个大人和4个小孩，共花了400元，李娜家去了4个大人和2个小孩，共花了400元，王斌家计划去3个大人和2个小孩，请你帮助他算一下，需要准备多少门票钱？（ ）
| A． | 300元 | B． | 310元 | C． | 320元 | D． | 330元 |
10．已知方程组$\left\{\begin{array}{l}{a_1}x+y={c_1}\\{a_2}x+y={c_2}\end{array}\right.$的解是$\left\{\begin{array}{l}x=5\\ y=10\end{array}\right.$；则关于x，y的方程组$\left\{\begin{array}{l}{a_1}x-y={a_1}+{c_1}\\{a_2}x-y={a_2}+{c_2}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}x=6\\ y=10\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=6\\ y=-10\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=-6\\ y=10\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=-6\\ y=-10\end{array}\right.$ |
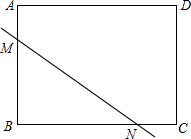在矩形ABCD中，AB=6，AD=8，把矩形ABCD沿直线MN翻折，点B落在边AD上的E点处．若AE=2AM，那么EN的长等于3$\sqrt{5}$．
8．
如图，在平行四边形ABCD中，AB=3，AD=2，则CD=（ ）
如图，在平行四边形ABCD中，AB=3，AD=2，则CD=（ ）| A． | 3 | B． | 2 | C． | 1 | D． | 5 |